I’m excited that our paper “A Semidefinite Relaxation for Sums of Heterogeneous Quadratic Forms on the Stiefel Manifold” has been published in the SIAM Journal on Matrix Analysis and Applications. https://doi.org/10.1137/23M1545136. We were inspired to work on this problem after it popped up inside the heteroscedastic PCA problem. It’s a fascinating, simple, general problem with connections to PCA, joint diagonalization, and low-rank semidefinite programs. Applying the standard Schur relaxation to this problem gives a trivial (and incorrect) solution, but one minor change makes the relaxation powerful and even tight in many instances. You can find the code for experiments here.
Recent News
Monarch Attention
June 6, 2025 By Laura Balzano
The attention module in transformer architectures is often the most computation and memory intensive unit. Many researchers have tried different ways to approximate softmax attention in a compute efficient way. We have a new approach that uses the Monarch matrix structure along with variational softmax to quickly and accurately approximate softmax attention in a zero-shot setting. The results are very exciting — we can significantly decrease the compute and memory requirements while taking at most a small hit to performance. This figure shows the performance versus computation of our “Monarch-Attention” method as compared to Flash Attention 2 (listed as “softmax”) and other fast approximations.
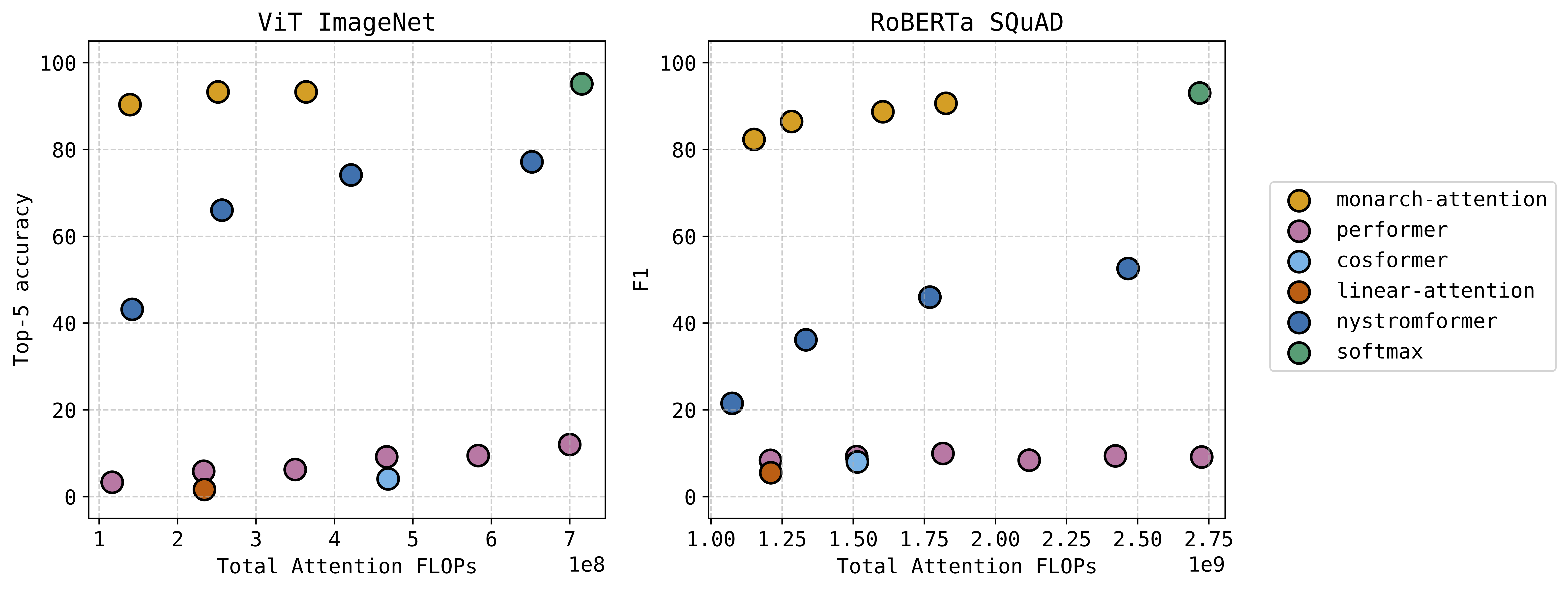
See the paper for additional results, including hardware benchmarking against Flash Attention 2 on several sequence lengths.
Can Yaras, Alec S. Xu, Pierre Abillama, Changwoo Lee, Laura Balzano. “MonarchAttention: Zero-Shot Conversion to Fast, Hardware-Aware Structured Attention.”
https://arxiv.org/abs/2505.18698
Code can be found here.
Analyzing Out-of-Distribution In-Context Learning
May 29, 2025 By Laura Balzano
We posted a new paper on arxiv presenting analysis on the capabilities of attention for in-context learning. There are many perspectives out there on whether it’s possible to do in-context learning out-of-distribution: some papers show it’s possible, and others do not, mostly with empirical evidence. We provide some theoretical results in a specific setting, using linear attention to solve linear regression. We show a negative result that when the model is trained on a single subspace, the risk on out-of-distribution subspaces is lower bounded and cannot be driven to zero. Then we show that when the model is instead trained on a union-of-subspaces, the risk can be driven to zero on any test point in the span of the trained subspaces – even ones that have zero probability in the training set. We are hopeful that this perspective can help researchers improve the training process to promote out-of-distribution generalization.
Soo Min Kwon, Alec S. Xu, Can Yaras, Laura Balzano, Qing Qu. “Out-of-Distribution Generalization of In-Context Learning: A Low-Dimensional Subspace Perspective.” https://arxiv.org/abs/2505.14808.
SDP Relaxation paper in SIMAX
April 19, 2025 By Laura Balzano
I’m excited that our paper “A Semidefinite Relaxation for Sums of Heterogeneous Quadratic Forms on the Stiefel Manifold” has been published in the SIAM Journal on Matrix Analysis and Applications. https://doi.org/10.1137/23M1545136. We were inspired to work on this problem after it popped up inside the heteroscedastic PCA problem. It’s a fascinating, simple, general problem with connections to PCA, joint diagonalization, and low-rank semidefinite programs. Applying the standard Schur relaxation to this problem gives a trivial (and incorrect) solution, but one minor change makes the relaxation powerful and even tight in many instances. You can find the code for experiments here.
© Copyright
Copyright © 2025 · Streamline Child Theme on Genesis Framework · WordPress · Log in