The attention module in transformer architectures is often the most computation and memory intensive unit. Many researchers have tried different ways to approximate softmax attention in a compute efficient way. We have a new approach that uses the Monarch matrix structure along with variational softmax to quickly and accurately approximate softmax attention in a zero-shot setting. The results are very exciting — we can significantly decrease the compute and memory requirements while taking at most a small hit to performance. This figure shows the performance versus computation of our “Monarch-Attention” method as compared to Flash Attention 2 (listed as “softmax”) and other fast approximations.

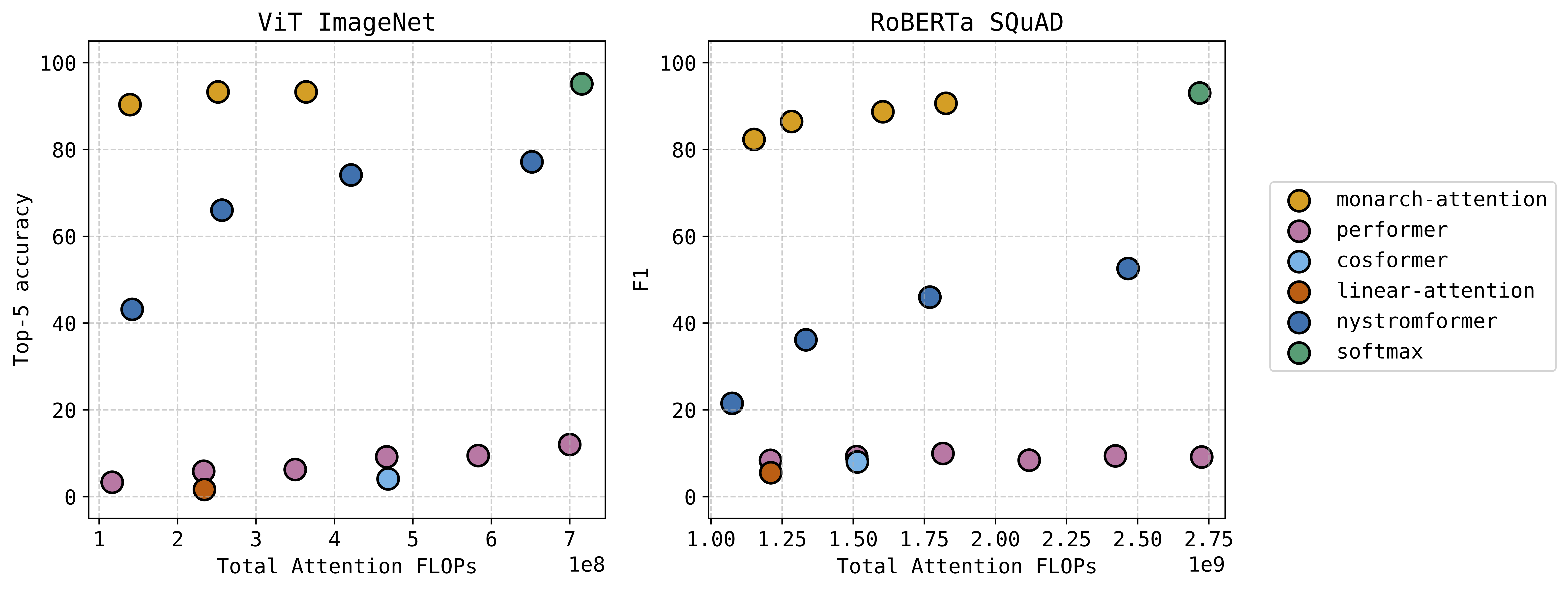
See the paper for additional results, including hardware benchmarking against Flash Attention 2 on several sequence lengths.

Can Yaras, Alec S. Xu, Pierre Abillama, Changwoo Lee, Laura Balzano. “MonarchAttention: Zero-Shot Conversion to Fast, Hardware-Aware Structured Attention.”
https://arxiv.org/abs/2505.18698
Code can be found here.

Our work on heteroscedastic PCA continues with our article “HePPCAT: Probabilistic PCA for Data with Heteroscedastic Noise,” published in IEEE Transactions on Signal Processing. In this paper we developed novel ascent algorithms to maximize the heteroscedastic PCA likelihood, simultaneously estimating the principal components and the heteroscedastic noise variances. We show a compelling application to air quality data, where it is common to have data both from sensors that are high-quality EPA instruments and others that are consumer grade. Code for the paper experiments is available at https://gitlab.com/heppcat-group, and the HePPCAT method is available as a registered Julia package. Congratulations to my student Kyle Gilman, former student David Hong, and colleague Jeff Fessler.

Kyle Gilman and I have a preprint out describing a new algorithm for online tensor completion and tracking. We derive and demonstrate an algorithm that operates on streaming tensor data, such as hyperspectral video collected over time, or chemo-sensing experiments in space and time. Kyle presented his work at the first fully virtual ICASSP, which you can view here. Anyone can register for free to this year’s virtual ICASSP and watch the videos, post questions, and join the discussion. Kyle’s code is also available here.

John Lipor, Andrew Gitlin, Bioashuai Tao, and I have a new paper, “Improving K-Subspaces via Coherence Pursuit,” to be published in the Journal of Special Topics in Signal Processing issue “Robust Subspace Learning and Tracking: Theory, Algorithms, and Applications.” In it we present a new subspace clustering algorithm, Coherence Pursuit – K-Subspaces (CoP-KSS). Here is the code for CoP-KSS and for our figures. Our paper considers specifically the PCA step in K-Subspaces, where a best-fit subspace estimate is determined from a (possibly incorrect) clustering. When a given cluster has points from multiple low-rank subspaces, PCA is not a robust approach. We replace that step with Coherence Pursuit, a new algorithm for Robust PCA. We prove that Coherence Pursuit indeed can recover the “majority” subspace when data from other low-rank subspaces is contaminating the cluster. In this paper we also prove — to the best of our knowledge, for the first time — that the K-Subspaces problem is NP-hard, and indeed even NP-hard to approximate within any finite factor for large enough subspace rank.