Congratulations to my student David Hong (and his co-advisor Jeff Fessler) for our published article in the Journal of Multivariate Analysis, titled “Asymptotic performance of PCA for high-dimensional heteroscedastic data.” Heteroscedastic data, where different data points are of differing quality (precisely, have different noise variance), are common in so many interesting big data problems. Sensor network data, medical imaging using historical data, and astronomical imaging are just a few examples. PCA is known to be the maximum likelihood estimate for data with additive Gaussian noise of a single variance across all the data points. This work investigates the performance of PCA when that homoscedastic noise assumption is violated. We give precise predictions for the recovery of subspaces and singular values in a spiked/planted model, and show that vanilla PCA (perhaps unsurprisingly) has suboptimal subspace recovery when the data are heteroscedastic.
Recent News
SPADA lab at Neurips 2025
December 8, 2025 By Laura Balzano
SPADA lab had two interesting works to share at Neurips this year. The first was MonarchAttention, which received a spotlight; thanks to everyone who stopped by the poster. See our earlier post for an example of how our method offers a zero-shot drop-in replacement for softmax attention at a significant savings of memory and computation – with very little accuracy loss. This technique has a University of Michigan patent pending.
The second work is on the topic of Out-of-Distribution In-Context Learning, which we presented at the What Can’t Transformers Do? Workshop. We analyze the solution for training linear attention on an out-of-distribution linear regression test task, where the training task is a regression vector either drawn from a single subspace or a union of subspaces. In the case of a union of subspaces, we can generalize to the span of the subspaces at test time.
Nice work to all the students: Can, Soo Min (both SPADA lab members), as well as our treasured collaborators Alec, Pierre, and Changwoo!
Monarch Attention
June 6, 2025 By Laura Balzano
The attention module in transformer architectures is often the most computation and memory intensive unit. Many researchers have tried different ways to approximate softmax attention in a compute efficient way. We have a new approach that uses the Monarch matrix structure along with variational softmax to quickly and accurately approximate softmax attention in a zero-shot setting. The results are very exciting — we can significantly decrease the compute and memory requirements while taking at most a small hit to performance. This figure shows the performance versus computation of our “Monarch-Attention” method as compared to Flash Attention 2 (listed as “softmax”) and other fast approximations.
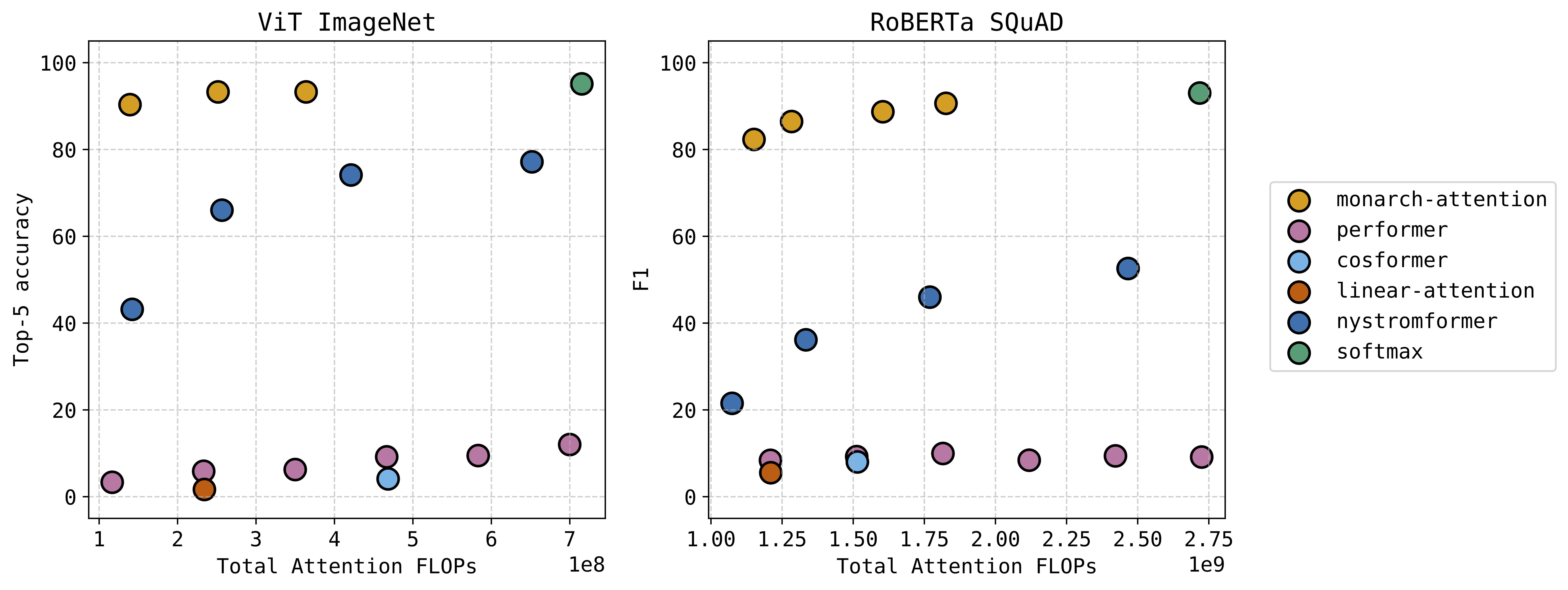
See the paper for additional results, including hardware benchmarking against Flash Attention 2 on several sequence lengths.
Can Yaras, Alec S. Xu, Pierre Abillama, Changwoo Lee, Laura Balzano. “MonarchAttention: Zero-Shot Conversion to Fast, Hardware-Aware Structured Attention.”
https://arxiv.org/abs/2505.18698
Code can be found here.
Analyzing Out-of-Distribution In-Context Learning
May 29, 2025 By Laura Balzano
We posted a new paper on arxiv presenting analysis on the capabilities of attention for in-context learning. There are many perspectives out there on whether it’s possible to do in-context learning out-of-distribution: some papers show it’s possible, and others do not, mostly with empirical evidence. We provide some theoretical results in a specific setting, using linear attention to solve linear regression. We show a negative result that when the model is trained on a single subspace, the risk on out-of-distribution subspaces is lower bounded and cannot be driven to zero. Then we show that when the model is instead trained on a union-of-subspaces, the risk can be driven to zero on any test point in the span of the trained subspaces – even ones that have zero probability in the training set. We are hopeful that this perspective can help researchers improve the training process to promote out-of-distribution generalization.
Soo Min Kwon, Alec S. Xu, Can Yaras, Laura Balzano, Qing Qu. “Out-of-Distribution Generalization of In-Context Learning: A Low-Dimensional Subspace Perspective.” https://arxiv.org/abs/2505.14808.
© Copyright
Copyright © 2026 · Streamline Child Theme on Genesis Framework · WordPress · Log in