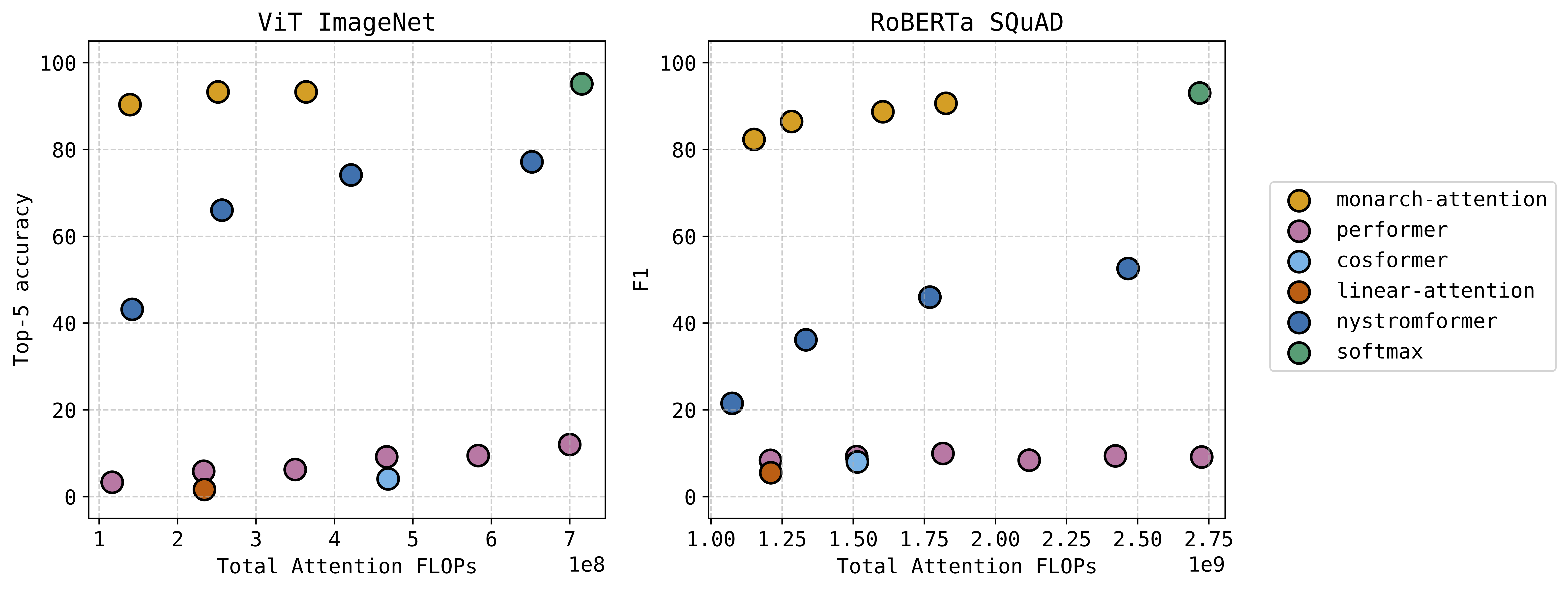
SPADA lab had two interesting works to share at Neurips this year. The first was MonarchAttention, which received a spotlight; thanks to everyone who stopped by the poster. See our earlier post for an example of how our method offers a zero-shot drop-in replacement for softmax attention at a significant savings of memory and computation – with very little accuracy loss. This technique has a University of Michigan patent pending.
The second work is on the topic of Out-of-Distribution In-Context Learning, which we presented at the What Can’t Transformers Do? Workshop. We analyze the solution for training linear attention on an out-of-distribution linear regression test task, where the training task is a regression vector either drawn from a single subspace or a union of subspaces. In the case of a union of subspaces, we can generalize to the span of the subspaces at test time.
Nice work to all the students: Can, Soo Min (both SPADA lab members), as well as our treasured collaborators Alec, Pierre, and Changwoo!