A Sparsification Approach to Set Membership Identification of Switched Affine Systems
N. Ozay, M. Sznaier, C. M. Lagoa, and O. I. Camps
IEEE Transactions on Automatic Control, March, 2012.
This paper addresses the problem of robust identification of a class of discrete-time affine hybrid systems, switched affine models, in a set membership framework. Given a finite collection of noisy input/output data and some minimal a priori information about the set of admissible plants, the objective is to identify a suitable set of affine models along with a switching sequence that can explain the available experimental information, while minimizing either the number of switches or subsystems. For the case where it is desired to minimize the number of switches, the key idea of the paper is to reduce this problem to a sparsification form, where the goal is to maximize sparsity of a suitably constructed vector sequence. Our main result shows that in the case of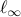 
bounded noise, this sparsification problem can be exactly solved via convex optimization. In the general case where the noise is only known to belong to a convex set 
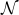, the problem is generically NP-hard. However, as we show in the paper, efficient convex relaxations can be obtained by exploiting recent results on sparse signal recovery. Similarly, we present both a sparsification formulation and a convex relaxation for the (known to be NP hard) case where it is desired to minimize the number of subsystems. These results are illustrated using two non-trivial problems arising in computer vision applications: video-shot and dynamic texture segmentation.