

Next: Equations for Reinforcement
Up: How to Make Software
Previous: The Elevator Problem
Reinforcement Learning (RL) corrects all three drawbacks of
the traditional approach. First, RL requires very little programmer
effort, because most of the work is done by a process of automatic
training, not programming. Second, if the environment changes, the
training can be re-run, without any additional programming. In fact,
retraining can be done continuously, online, as the system runs.
Third, RL is mathematically guaranteed to converge to an optimal
policy (given certain assumptions described later).
What does an agent need to know in order to take optimal
actions? Clearly, it would be a big help if the agent could predict
the reward function, the reward it would receive from taking
a given action in a given state. But that would not be enough.
Consider an empty elevator that is approaching the seventh floor on
its way up, and assume that there are passengers waiting to go down on
the seventh, eighth, and ninth floors. Stopping at the seventh floor
would give a larger immediate reward than either continuing on up or
reversing direction. But if we did stop at the seventh floor, we
would have to take the passenger there down, and return later for the
other passengers. A wiser strategy---one with a better
long-term reward---would be to bypass the seventh and eighth floors
and pick up the passengers on the ninth floor first and then go down,
picking up the passengers on the eighth and seventh floors on the way.
The problem is that the reward function just captures the
immediate or short-term consequences of executing actions. What we
need instead is a function that captures the long-term
consequences. Such a function is called a utility function.
Intuitively, the utility of taking action  in some state
in some state
 is the expected immediate reward for that action plus the sum of
the long-term rewards over the rest of the agent's lifetime, assuming
it acts using the best policy. Equations (1) and
(2) in Section 3.1 formally define the utility
function.
is the expected immediate reward for that action plus the sum of
the long-term rewards over the rest of the agent's lifetime, assuming
it acts using the best policy. Equations (1) and
(2) in Section 3.1 formally define the utility
function.
If we knew the utility function, then the optimal policy would
be to enumerate all possible actions and choose the action with the
highest utility. Solving the elevator problem therefore reduces to
learning the utility function. Theoretically, it is possible to
exactly solve for the utility function. Equation (3) in
Section 3.1 shows how the utility of a state is related to
immediate reward and the utility of the resulting state. If there are
n actions and m states, this defines a system of n m nonlinear
equations in n m unknowns, which can be solved by standard methods,
such as dynamic programming (Bertsekas [2]). In
practice, however, this rarely works.
One problem is that our simulation model of the elevator
system consists of probability distributions for passenger arrivals
and destinations, etc. In order to compute the expectations in
Equation 4 to do dynamic programming, we must first convert our
simulation model into a model of state transition probabilities. Doing
so is computationally expensive. Another problem is that in our
elevator example the state-transition probabilities are continuous, so
even if we had them, computing the expectations would be very
expensive. Finally, Equation 4 requires an iteration over the
entire state space of the system. Our elevator example has more than
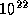 states --- iterating over all of them is impossible. If we
did not have a simulation model to begin with, doing dynamic
programming would first require estimating a model by experimenting
with the real elevator system.
states --- iterating over all of them is impossible. If we
did not have a simulation model to begin with, doing dynamic
programming would first require estimating a model by experimenting
with the real elevator system.
Reinforcement Learning is an iterative approach that
eliminates these problems to comes up with an approximate solution to
the utility function. The basic idea is to start with some initial
guess of the utility function, and to use experience with the elevator
system to improve that guess. To gain experience, one needs either a
simulated elevator system or the ability to select actions and acquire
data from the real elevator system. In either case, the experience
that the program acquires is a state-action trajectory with associated
rewards (see Figure 3). On each step through the trajectory,
the agent takes some action and receives some reward. The reward is
information that it can use to update its estimate of the utility
function, according to Equation (5) in Section 3.1.
By focusing computation on the states that actually occur in the
simulation, RL is able to deal with larger state spaces than dynamic
programming methods. As the program gains more experience, the
difference between its estimated utility function and the true utility
function decreases.
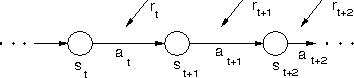
Figure: The program's experience consists of a trajectory through
state space. At time step t, the state is 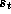 and the agent faces
a choice of actions. Denote the action the agent chooses to execute at
step t as
and the agent faces
a choice of actions. Denote the action the agent chooses to execute at
step t as 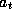 . The reward at step t,
. The reward at step t, 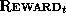 , is a function
of
, is a function
of 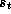 and
and 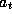 . The next state
. The next state 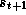 depends on
depends on
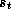 ,
, 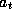 and many random things such as passengers arriving
at floors and pushing buttons. Reinforcement learning
allows a program to use such a trajectory to incrementally improve its
policy.
and many random things such as passengers arriving
at floors and pushing buttons. Reinforcement learning
allows a program to use such a trajectory to incrementally improve its
policy.
We are finally able to say exactly how RL allows us to write
an elevator control program:
(1) Code up a simulation of the elevator system. Make some
measurements or estimates of passenger arrival rates and other
parameters, and write a program to simulate the elevator environment.
(2) Determine the reward function.
(3) Make an initial guess at a utility function. This can be based on
simple rules like ``it is better to move up if there is a passenger
waiting above.'' The details are not important, because the guess
will be improved.
(4) Run the simulation, updating the utility function on each step
using Equation (5). Given enough time to explore in the
simulated system, our program will converge to a near-optimal policy.
(5) The final version of the program can then be used to control the
real elevator system. If desired, the program could continually monitor
its performance and update its utility function to reflect changes in
the real environment.


Next: Equations for Reinforcement
Up: How to Make Software
Previous: The Elevator Problem
 in some state
in some state
 is the expected immediate reward for that action plus the sum of
the long-term rewards over the rest of the agent's lifetime, assuming
it acts using the best policy. Equations (1) and
(2) in Section 3.1 formally define the utility
function.
is the expected immediate reward for that action plus the sum of
the long-term rewards over the rest of the agent's lifetime, assuming
it acts using the best policy. Equations (1) and
(2) in Section 3.1 formally define the utility
function.


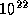 states --- iterating over all of them is impossible. If we
did not have a simulation model to begin with, doing dynamic
programming would first require estimating a model by experimenting
with the real elevator system.
states --- iterating over all of them is impossible. If we
did not have a simulation model to begin with, doing dynamic
programming would first require estimating a model by experimenting
with the real elevator system.
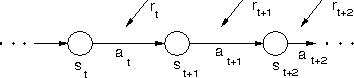
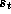 and the agent faces
a choice of actions. Denote the action the agent chooses to execute at
step t as
and the agent faces
a choice of actions. Denote the action the agent chooses to execute at
step t as 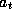 . The reward at step t,
. The reward at step t, 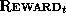 , is a function
of
, is a function
of 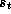 and
and 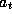 . The next state
. The next state 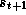 depends on
depends on
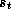 ,
, 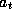 and many random things such as passengers arriving
at floors and pushing buttons. Reinforcement learning
allows a program to use such a trajectory to incrementally improve its
policy.
and many random things such as passengers arriving
at floors and pushing buttons. Reinforcement learning
allows a program to use such a trajectory to incrementally improve its
policy.