As an example, consider the problem of programming a bank of elevators (borrowed from Crites and Barto [3]). Consider a ten floor building with three elevators (Figure 1). What program should we write to control them? By this, we don't mean what programming language, or what hardware configuration we should use --- though those are certainly important questions. Instead, we mean the more fundamental question of how we approach the programming task.
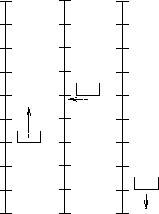
Figure: The Elevator Problem. A building with ten floors and three
elevators. The software program is to control the actions of each
elevator. The information available to the program are the state of
each button on the floors and inside the elevators, as well as the
time elapsed since each floor-button push.
We will think of this as an agent-based program. Once every, say, 1/2 second, the program will examine the information available to the elevator sensors, and decide what actions the elevators should take. The sensor information or percepts include the buttons which are lit on each floor and inside each elevator. (Some more advanced elevators can detect the weight of the passengers in each car and the breaking of an electric eye beam at each door, but we'll assume our elevators do not.) An empty elevator can either stop, go up, or go down. One constraint, driven by passenger expectation, is that a non-empty elevator must continue in its current direction and stop at all the floors requested by its passengers before it reverses directions. We assume that we don't need to explicitly control the doors: they will always open when the elevator is stopped at a floor with a corresponding lit button, and close before the elevator moves.
We could use separate agents for each elevator, but for the moment let us assume that there is one central program. On each iteration, the program receives as percepts an on or off signal for each button, and the current floor and direction of each elevator. The program's output is a list of actions, one for each elevator, e.g., [ up, stop, up], that obey the constraints stated above.
In most complex problems, the percepts alone are not enough to decide on good actions. For example, it is useful to know how long a passenger has been waiting for an elevator to arrive. Since this is not available from the percepts, the system will need to have some memory. Let us use the term state to denote the available information, both percept and memory (in control theory, ``state'' implies certain technical constraints which we ignore for simplicity; see Barto, Bradtke and Singh [1]). The program's behavior is a feedback-loop (Figure 2). At each time step, the program has access to the current state of the system and has to decide what action to execute. After each action, the system moves to a new state, and the decision process is repeated. Technically, we say that a mapping from the space of states to the space of actions is a policy. Our problem is that of finding an optimal or near-optimal policy.
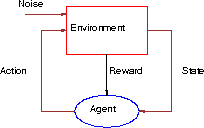
Figure: Abstract Agent Program. The program interacts with an
environment in a feedback cycle. At each step, the agent perceives
part of the environment (and may remember some), executes an action,
and receives a reward. The environment changes to a new state, which
is partially determined by the action (elevators move up or down) and
partially unpredictable (buttons are pushed). The agent's goal is to
execute actions to maximize the reward it accumulates over time.
What is optimal? There are many criteria we could consider: the number of passengers delivered to their destination, the time a passenger waits for an elevator to arrive, the time spent inside the elevator, the cost of the power consumed by the system, the wear and tear from moving and reversing directions, etc (or the resulting time and money spent on maintenance). Typically there are trade-offs among these; reducing wear and tear may increase wait time. Some criteria are best thought of as costs to be minimized while others are rewards to be maximized, but it will simplify things if we treat them all as rewards, with the understanding that a cost is treated as a negative reward.
We can then define an optimal policy as one that maximizes the expected sum of the rewards it receives over its lifetime. (Here, expected means that we have to average over all sources of randomness in the system; in complex systems the reward you get often depends on many random factors beyond the agent's control. In the elevator system, the number of passengers and their arrival and destination floors are random.)
Let's assume we want to minimize two quantities: the time spent by passengers waiting for an elevator, and the distance traveled by the elevators (which effects both energy and maintenance costs). To put this into the language of rewards, we need a common scale for the two quantities. For concreteness, let's say that on each time step we will receive a reward of -50 for every floor that has passengers waiting, and -1 for every elevator in motion.
In the traditional approach to this problem, the programmer would come up with a set of rules and procedures on when to take what action based on common-sense or rough heuristics. There are three drawbacks of this approach. First, it requires a lot of work on the part of the programmer. Second, when the environment changes in some way (perhaps faster elevators are installed), a programmer needs to be called in again. Third, there's no way to guarantee that this will lead to an optimal policy; sometimes common sense is just wrong. Even if the rules and procedures are quite sensible in general, they would not pay any attention to the traffic patterns of a particular building, which means they might be missing an opportunity for fine-tuning.