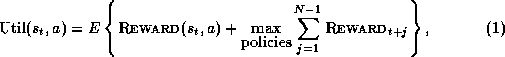
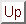
Utility (over a finite agent lifetime) is defined as the expected sum of the immediate reward and the long-time reward under the best possible policy:
where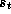 
is the state at time step t, 
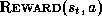is the
immediate reward of executing action 
in state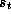 
, N is
the number of steps in the lifetime of the agent, and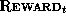 
is the
reward at time step t.). The operator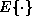 
stands for
taking an expectation over all sources of randomness in the system.
Utility (over an infinite agent lifetime) is defined similarly:
To avoid the mathematical awkwardness of infinite sums, we introduce a
discount factor,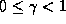 
, which counts future rewards less
than immediate rewards. This is similar to the compound interest that
banks use.
The utility of a state can be defined in terms of the utility of the next state:
This gives a system of equations, called the Bellman Optimality Equations (e.g., Bertsekas [2]), one for each possible state-action pair, the solution to which is the utility function.
The dynamic programming method for solving the Bellman equations is to
iterate the following,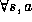 
:
The RL rule for updating the estimated utility is:
where 
is a small number less than one that determines the
rate of change of the estimate. Notice that the second part of
Equation 5 is a lot like Equation 3, except that
there are no expectation signs E anywhere. See Barto, Bradtke, and
Singh [1] for additional information
on RL methods.
