cs1120 Problem Set 3:
Limning L-System Fractals
- Bring in to class a stapled turn-in containing your written answers to all the questions. If you worked with a partner, you and your partner should submit a single writeup with both of your names and UVA Email Ids on it. You must clearly indicate both names and UVA IDs in big block letters if you are working in a team.
- Use our automatic adjudication service to submit a single Python file (a modification of ps3.py) containing all your code answers. You must define an author list. Each partner must separately submit a copy of your joint file.
- Use our automatic adjudication service to submit a single Python file and a single SVG image file as your answer to Question 11. You must define an author list. Each partner must separately submit copies of the files. For this problem, partners may submit separate fractals if they choose.
Collaboration Policy - Read Carefully
For this problem set, you may choose to work with a partner of your choice. You are not required to do so.Before starting to work with a partner, you should go through questions 1 and 2 yourself on paper. When you meet with your partner (if any), check if you made the same predictions. If there are any discrepancies, try to decide which is correct before using Python to evaluate the expressions.
If you have a partner, you and your partner should work together on the rest of the assignment. You should read the whole problem set yourself and think about the questions before beginning to work on them with your partner. Both partners need to understand everything you submit.
Remember to follow the pledge you read and signed at the beginning of the semester. For this assignment, you may consult any outside resources, including books, papers, web sites and people, you wish except for materials from previous cs1120, cs150, and cs200 courses. You may consult an outside person (e.g., another friend who is a CS major but is not in this class) who is not a member of the course staff, but that person cannot type anything in for you and all work must remain your own. That is, you can ask general questions such as "can you explain recursion to me?" or "how do lists work in Python?", but outside sources should never give you specific answers to problem set questions. If you use resources other than the class materials, lectures and course staff, explain what you used in your turn-in.
You are strongly encouraged to take advantage of the scheduled help hours and office hours for this course.
Purpose
- Practice programming with recursive definitions and procedures
- Explore the power of rewrite rules
- Write recursive functions that manipulate lists
- Make a cs1120 course logo better than "The Great Lambda Tree of Infinite Knowledge and Ultimate Power"
Optional Reading: Complete Units 1 through 3 of Udacity Introduction to Computing.
- ps3.py — A template for your answers. You should do the problem set by editing this file.
- graphics.py — Python code for L-System fractals and drawing curves. You should read and understand most of this file.
- canvasvg.py — provided library code for saving your fractals as image files on disk. You do not need to read or understand this file.
Background
In this problem set, you will explore a method of creating fractals known as the Lindenmayer system (or L-system). Aristid Lindemayer, a theoretical biologist at the University of Utrecht, developed the L-system in 1968 as a mathematical theory of plant development. In the late 1980s, he collaborated with Przemyslaw Prusinkiewicz, a computer scientist at the University of Regina, to explore computational properties of the L-system and developed many of the ideas on which this problem set is based.
The idea behind L-system fractals is that we can describe a curve as a list of lines and turns, and create new curves by rewriting old curves. Everything in an L-system curve is either a forward line (denoted by F), or a right turn (denoted by Ra where a is an angle in degrees clockwise). We can denote left turns by using negative angles.
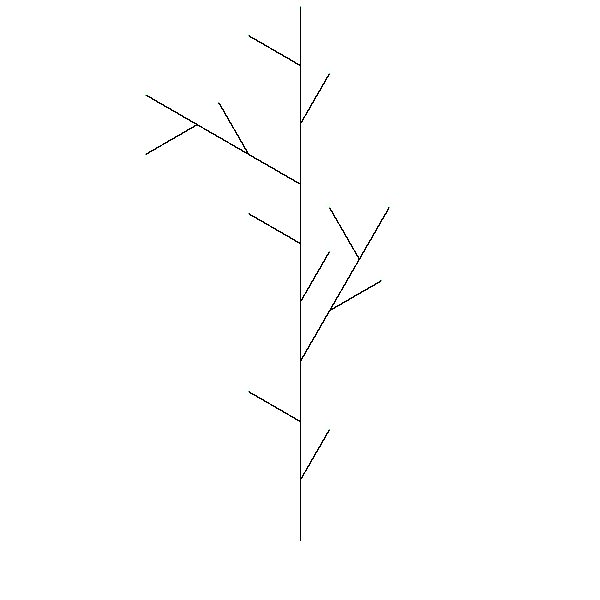
We create fractals by recursively replacing all forward lines in a curve list with the original curve list. Lindemayer found that many objects in nature could be described using regularly repeating patterns. For example, the way some tree branches sprout from a trunk can be described using the pattern: F O(R30 F) F O(R-60 F) F. This is interpreted as: the trunk goes up one unit distance, a branch sprouts at an angle 30 degrees to the trunk and grows for one unit. The O means an offshoot — we draw the curve in the following parentheses, and then return to where we started before the offshoot. The trunk grows another unit and now another branch, this time at -60 degrees relative to the trunk grows for one units. Finally the trunk grows for one more unit. The branches continue to sprout in this manner as they get smaller and smaller, and eventually we reach the leaves.
We can describe this process using replacement rules:
Start: [F]Here are the commands this produces after two iterations:
Rule: F ::= [F O[R30 F] F O[R-60 F] F]
Iteration 0: [F]
Iteration 1: [F O[R30 F] F O[R-60 F] F]
Iteration 2: [F O[R30 F] F O[R-60 F] F O[R30 F O[R30 F] F O[R-60 F] F] F O[R30 F] F O[R-60 F] F O[R-60 F O[R30 F] F O[R-60 F] F] F O[R30 F] F O[R-60 F] F]
Here's what that looks like:
|
 Iteration 5 (with color) The Great Lambda Tree of Infinite Knowledge and Ultimate Power |
Note that L-system command rewriting is similar to the replacement rules in a BNF grammar. The important difference is that with L-system rewriting, each iteration replaces all instances of F in the initial string instead of just picking one to replace.
We can divide the problem of producing an L-system fractal into two main parts:
- Produce a list of L-system commands that represents the fractal by rewriting according to the L-system rule; and
- Drawing a list of L-system commands.
Representing L-System Commands
Here is a BNF grammar for L-system commands:
- CommandSequence ::= [ CommandList ]
- CommandList ::= Command CommandList
- CommandList ::=
- Command ::= F
- Command ::= RAngle
- Command ::= O CommandSequence
- Angle ::= Number
We need to find a way to turn strings in this grammar into lists and objects we can manipulate in a Python program. We will use a list of lists to represent a CommandList and a list of strings to represent different commands. For example, the list ['F'] will denote forward, ['R', angle] will denote a rotation, and ['O', CommandList] will denote an offshoot.
# Command ::= F def make_forward_command(): return ['F'] # creates a list of one element, 'F' # Command ::= R Angle def make_rotate_command(angle): return ['R', angle] # creates a list of two elements, 'R' and a number # Command ::= O CommandSequence def make_offshoot_command(commandsequence): return ['O', commandsequence] # creates a list of two elements, 'O' and another list
- is_forward(lcommand) — evaluates to True if the parameter passed is a forward command (indicated by its first element being a 'F'). Evaluates to False otherwise.
- is_rotate(lcommand)
- is_offshoot(lcommand)
- get_angle(lcommand) — evaluates to the angle associated with a rotate command. Produces an error if the command is not a rotate command (see ps3.py for how to produce an error).
- get_offshoot_commands(lcommand) — evaluates to the offshoot command list associated with an offshoot command. Produces an error if the command is not an offshoot command.
>>> is_forward(make_forward_command()) True >>> is_forward(make_rotate_command(90)) False >>> get_angle(make_rotate_command(90)) 90 >>> get_angle(make_forward_command()) # ERRORYou should be able to make up similar test cases yourself to make sure the other procedures you defined work.
New Python Special Forms
The code for this problem set introduces a few new Python tools. None of these new forms are necessary for expressing important computations, but they make it easier or more concise to express some ideas. We will introduce three new Python concepts and then return to reasoning about fractals.
New Python Syntax: elif
When we have if else statements, there are two branches we can take: the if-branch and the else-branch. We can use elif (short for "else if") statements if we want to have more than just two branches in our program. For example, nucleotide_complement from Problem Set 2 mighit be written with elif:
if letter == 'G':
return 'C'
elif letter == 'C':
return 'G'
elif letter == 'A':
return 'T'
else: # must be 'T'
return 'A'
Answer this question by providing a written formal argument. Although the idea may be conceptually clear, we will grade this question harshly if you do not formally address some possible case. Strive to make your answer as general as and formal as possible. For example, just showing how the nucleotide_complement example above (one example) could be written does not necessarily handle all possible cases.
We don't need to know how to use elif statements, but if we use them, our code can become shorter and more readble — especially if the number of conditional branches is high.
New Python Concept: Global Variables
Thus far in the course we have used local variables. A local variable is a variable that lives inside of a function, and dies when the program execution leaves that function. Python de-allocates the memory storage used to hold a local variable when we are done with its function. (In later lectures we will eventually define a formal notion of scope that explains this process.)By contrast, a global variable is a variable that lives outside of any function and can be referenced anywhere in the program. Python has a special way to do this, but using global variables is typically considered bad programming practice (i.e., "bad style" or "ugly"). You should not use global variables but you should know that they exist and how they work.
my_variable = 5 # Initialize a global variable.
# Note that this variable is defined
# outside of the body of any function.
def change_the_value_of_my_variable(x):
# We must tell Python that we want access to our global variable.
# This next line, starting with the keyword syntax "global",
# does just that.
global my_variable
# Now we if we assign a new value to our global variable, that
# assignment will live on even after this function finishes.
my_variable = x
def common_bug(x):
# If we forget to say "global", Python will instead make a
# new local variable that just happens to have the same name!
my_variable = x
# The above assignment does not change our global variable.
print(my_variable)
change_the_value_of_my_variable(7)
print(my_variable)
common_bug(10)
print(my_variable)
This code will print 5, 7, and 7.
New Python Concept: Functions nested within other functions
Recall from the lectures that lambda can be used to create an anonymous function. For example:>>> square = lambda(t) : t * t >>> print square(5) 25We can even write procedures that return functions created by lambda:
>>> def make_adder(a):
return lambda(b) : a + b
>>> add_three = make_adder(3)
>>> print add_three(4)
7
>>> print add_three(-2)
1
We don't have to use lambda, however. The previous example is equivalent
to:
>>> def make_adder(a):
def adder(b):
return a + b
return adder
>>> add_three = make_adder(3)
>>> print add_three(4)
7
>>> print add_three(-2)
1
>>> print adder(3)
# ERROR: adder is not visible at the outermost level.
# You can only refer to it by name inside of make_adder!
In the above example, the function adder is defined nested
inside the functino make_added.
While lambda is very convenient, Python will not allow us to put more than one line of code in the body of a lambda — for example, you may have noticed that lambda implicitly returns its body, so you can't use our usual if statement inside a lambda. Nested functions allow us to write more complicated code such as loops and conditional statements. In the code for this problem set, graphics.py has many examples of nested functions.
Having introduced these three new Python concepts, we now have everything we need to get back to drawing fractals!
Rewriting Curves
The power of the L-System commands comes from the rewriting mechanism. Recall how we described the tree fractal:Start: [F]To produce levels of the tree fractal, we need a procedure that takes a list of L-system commands and replaces each F command with the list of L-system commands given by the rule.
Rule: [F] ::= [[F], [O, [[R, 30], [F]]], [F], [O, [[R,60], [F]], [F]]]
So, for every command in the list:
- If the command is an F command, replace it with the replacement commands
- If the command is an RAngle command, keep it unchanged
- If the command is an OCommandSequence command, recursively rewrite every command in the offshoot's command list the same way
For example, consider a simple L-System rewriting:
Start: [F]We want to get:
Rule: [F] ::= [[F], [R, 30], [F]]
Iteration1: [[F], [R, 30], [F]]However, if we naively replace each [F] with [[F], [R, 30] [F]] lists, we would get something a little different:
Iteration2: [[F], [R, 30], [F], [R, 30], [F], [R, 30], [F]]
Iteration1: [[[F], [R, 30], [F]]]Notice that there are "too many [ ]'s". The easiest way to fix this problem is to flatten the result. The code should look similar to many recursive list procedures you have seen (this code is provided for you in lsystem.py):
Iteration2: [[[F], [R, 30], [F]], [R, 30], [[F], [R, 30], [F]]]
def flatten_commands(ll):
if len(ll) == 0:
return ll
elif is_lsystem_command(ll[0]):
return [ll[0]] + flatten_commands(ll[1:])
else:
x = [flatten_commands(ll[0])] + flatten_commands(ll[1:])
return x[0] + x[1:]
Hint: You'll have to handle both forward commands and also offshoot commands specially.
If you define these procedures correctly, you should produce these evaluations:
>>> rewrite_lcommands(['F'], [['F'],['R', 30], ['F']]) [['F'],['R', 30], ['F']] >>> rewrite_lcommands([['F'],['R', 30], ['F']], [['F'], ['F'], ['R', 30]]) [['F'], ['F'], ['R', 30], ['R', 30], ['F'], ['F'], ['R', 30]]
To make interesting L-system curves, we will need to apply rewrite_lcommands many times. We will leave that until the last question. Next, we will work on turning sequences of L-system commands into curves we can draw.
Drawing L-System Fractals
To draw our L-system fractals, we will need procedures for drawing curves. There are many different ways of thinking about curves. Mathematicians sometimes think about curves as functions from an x coordinate value to a y coordinate value. The problem with this way of thinking about curves is there can only be one y point for a given x point. This makes it impossible to make simple curves like a circle where there are two y points for every x value on the curve. So, a more useful way of thinking about curves is as functions that map numbers to [x,y] points. We can produce infinitely many different points on the curve by evaluating the curve function with the (infinitely many different) real numbers between 0 and 1 inclusive.You can think of the number between 0 and 1 as time — the first point of the curve you draw will be the point returned by curve(0.0), the middle part of the curve you draw will be the point returned by curve(0.5), and the last part of the curve you draw will be the point returned by curve(1.0).
Of course, we can't really evaluate the curve function at every value between 0 and 1 (because there are infinitely many of them — it would take too long!). Instead, we will evaluate it at a large number of points distributed between 0 and 1 to display an approximation of the curve.
Points
We need a way to represent the points on our curves. A point is a pair of two values, x and y representing the horizontal and vertical location of the point.We will use a coordinate system from (0, 0) to (1, 1):
| (0.0, 1.0) | (1.0, 1.0) | ||
|
|
|||
| (0.0, 0.0) | (1.0, 0.0) |
Points have x and y coordinates. To represent points we would like to define procedures make_point, x_of_point and y_of_point. We will use lists to represent points. Our pictures will be more interesting if points can have color too. So, we represent a colored point using a list of three values: x, y and color:
def make_point(x,y):
return [x,y, (0,0,0)] # (0,0,0) is the red-green-blue color "black"
def make_colored_point(x,y,c):
return [x,y,c]
def x_of_point(point):
return point[0]
def y_of_point(point):
return point[1]
def color_of_point(point):
return point[2]
We have provided some procedures for drawing on the window in graphics.py:
- window_draw_point(point) — Draw the point on the window. For example, window_draw_point(make_point(0.5, 0.5)) will place a black dot in the center of the window. (The point is only one pixel, so it is hard to see.)
- window_draw_line(point0, point1) — Draw a black line from point0 to point1. For example, window_draw_line(make_point(0.0, 0.0), make_point(1.0, 1.0)) will draw a diagonal line from the bottom left corner to the top right corner.
Read through graphics.py and look for other handy functions.
Drawing Curves
Building upon points, we can make curves and lines (straight lines are just a special kind of curve). Curves are procedures from values to points. One way to represent a curve is as a procedure that returns a point for every input value between 0.0 and 1.0. Remember that the input value can be thought of as representing time: the first point returned at 0.0 is the first one you draw, the point returned at 1.0 is the last one you draw. For example, the following curve
def mid_line(time)
return make_point(time, 0.5)
defines a curve that is a horizontal line across the middle of the
window. If we apply mid_line to a value x, we get
the point (x, 0.5). Hence, if we apply
mid_line to all values between 0.0 and 1.0, we get a
horizontal line.
Predict what x_of_point(mid_line(0.7)) and y_of_point(mid_line(0.7)) should evaluate to. Try evaluating them in Pycharm.
Of course, there are infinitely many values between 0.0 and 1.0, so we can't apply the curve function to all of them. Instead, we select enough values to show the curve well. To draw a curve, we need to apply the curve procedure to many values in the range from 0.0 to 1.0 and draw each point it evaluates to. Here's a procedure that does that:
def draw_curve_points(curve, n):
for step in range(n): # range(n) = [0, 1, 2, ..., n-1]
time = 1.0 * step / n
window_draw_point(curve(time))
# For exmaple, if n=5, we will draw the curve with time =
# 0, 0.2, 0.4, 0.6, and 0.8
# ... which are five times "evenly distributed" between 0.0 and 1.0.
The procedure draw_curve_points takes a procedure representing a
curve, and n, the number of points to draw. It uses
for step in range(n) to draw n evenly spaced points for the curve.
- Define a procedure, vertical_mid_line that can be passed
to draw_curve_points so that
draw_curve_points(vertical_mid_line, 1000) produces
a vertical line in the middle of the window.

- Define a procedure, make_vertical_line that takes one parameter
and produces a procedure that produces a vertical line at that
horizontal location. For example, draw_curve_points(make_vertical_line(0.5), 1000)
should produce a vertical line in the middle of the window and
draw_curve_points(make_vertical_line(0.2), 1000) should produce a
vertical line near the left side of the window:

Manipulating Curves
The good thing about defining curves as procedures is it is easy to modify and combine then in interesting ways.For example, the procedure rotate_ccw takes a curve and rotates it 90 degrees counter-clockwise by swapping the x and y points:
def rotate_ccw(curve):
def new_curve(t):
ct = curve(t)
return make_point(y_of_point(ct),x_of_point(ct))
return new_curve
Note that (rotate_ccw c) evaluates to a new curve that is just like the old curve c but rotated. The function rotate_ccw is a procedure that takes a procedure (a curve) and returns a procedure that is a curve. We created a new local variable, ct, and set it to curve(t) so that we didn't have to call curve(t) two times to get both the x- and the y-value at time t.
Predict what draw_curve_points(rotate_ccw(mid_line), 1000) and draw_curve_points(rotate_ccw(rotate_ccw(mid_line)), 1000) will do. Confirm your predictions by trying them in Pycharm.
(You may have just read over that paragraph and not actually done the prediction. The instructions are not just there to waste time: experience suggests that students who do not do them become confused on subsequent Questions and then come back. Thus you can save time by doing them now! If you already did them, great work!)
Here's another example:
def shrink(curve, scale):
# For example, scale = 0.25 may mean "one-quarter normal size"
def new_curve(t):
ct = curve(t)
return make_point(scale*x_of_point(ct), scale*y_of_point(ct))
return new_curve
Predict what draw_curve_points(shrink(mid_line, 0.5), 1000)
will do, and then try it in Pycharm.
The shrink procedure doesn't produce quite what we want because in addition to changing the size of the curve, it moves it around. Why does this happen? Try shrinking a few different curves to make sure you understand why the curve moves.
One way to fix this problem is to center our curves around (0,0) and then translate them to the middle of the screen. In mathematics and geometry, translation means moving a shape without rotating or flipping it. That is, to translate a curve is to "slide" it. We can do this by adding or subtracting constants to the points they produce:
def translate(curve, delta_x, delta_y):
def new_curve(t):
ct = curve(t)
return make_colored_point(delta_x+x_of_point(ct), \
delta_y+y_of_point(ct), color_of_point(ct))
return new_curve
Now we have translate, it makes more sense to define
mid_line this way:
def horiz_line(t):
return make_point(t, 0)
mid_line = translate(horiz_line, 0, 0.5)
When you are done, draw_curve_points(half_line, 1000) should produce a horizontal line that starts in the middle of the window and extends to the right boundary.

Hint: If you do not see anything when you are drawing a curve, it may be that you haven't yet applied translate and the points are being drawn along the bottom edge of the screen.
In addition to altering the points a curve produces, we can alter a curve by changing the time values it will see. For example,
def first_half(curve): return (lambda(time) : curve(time / 2))is a function that takes a curve and produces a new curve that only draws the first half of the input curve.
Predict what each of these expressions will do:
- draw_curve_points(first_half(mid_line), 1000)
- draw_curve_points(first_half(first_half(mid_line)), 1000)
The provided code includes several other functions that transform
curves including:
- scale_x_y(curve, x_scale, y_scale) — evaluates to curve stretched along the x and y axis by using the scale factors given
- scale(curve, scale) — evaluates to curve stretched along the x and y axis by using the same scale factor
- rotate_around_origin(curve, degrees) — evaluates to curve rotated counterclockwise by the given number of degrees.
It is also useful to have curve transforms where curves may be combined. An example is connect_rigidly(curve1, curve2) which evaluates to a curve that consists of curve1 followed by curve2. The starting point of the new curve is the starting point of curve1 and the end point of curve2 is the ending point of the new curve. Here's how connect_rigidly is defined:
def connect_rigidly(curve1, curve2):
def new_curve(t):
# We'll split our time between drawing curve1 and
# drawing curve2.
if(t < 0.5):
# When we think it's time 0.0 to 0.5, we'll draw
# curve1 so that curve1 thinks it's time 0.0 to 1.0.
return curve1(2*t)
else:
# When we think it's time 0.5 to 1.0, we'll draw
# curve2 so that curve2 thinks it's time 0.0 to
# 1.0.
return curve2(2*t - 1)
return new_curve
Note that connect_rigidly gives half of its "time budget" to
curve1 and half to curve2, so when we call draw_curve_points(..., n)
we'll may want to double the value of n. We'll return to this issue
in a bit.
Predict what draw_curve_points(connect_rigidly(vertical_mid_line, mid_line), 1000) will do. Is there any difference between that and draw_curve_points(connect_rigidly(mid_line, vertical_mid_line), 1000)? Check your predictions in Pycharm.
Distributing t Values
The way connect_rigidly is defined above, we use all the t-values below 0.5 on the first curve, and use the t-values between 0.5 and 1.0 on the second curve. If the second curve is the result of connecting two other curves, like connect_rigidly(c1, connect_rigidly (c2, c3)) then 50% of the points will be used to draw c1, 25% to draw c2 and 25% to draw c3.Consider connect_rigidly(A, connect_rigidly(B, C)) — A will get half of the time points and B and C will each get only one quarter of them. (If you're not sure why, take another look at the connect_rigidly code.) That means that B and C will look dotty or grainy compared to A.
This isn't too big a problem when only a few curves are combined; we can just increase the number of points passed to draw_curve_points to have enough points to make a smooth curve. In this problem set, however, you will be drawing fractal curves made up of thousands of connected curves. Just increasing the number of points won't help much, as you'll see in Question 7.
connect_rigidly(c1, connect_rigidly(c2, connect_rigidly(c3, ... cn)))The first argument to num_points is the number of t-values left. The second argument is the number of curves left.
Think about this yourself first, but look in ps3.py for a hint if you are stuck. There are mathematical ways to calculate this efficiently, but the simplest way to calculate it is to define a procedure that keeps halving the number of points n times to find out how many are left for the nth curve.
Your num_points procedure should produce results similar to:
>>> num_points(1000,10) 1.953125 >>> num_points(1000,20) 0.00190734863281 >>> num_points(1000000,20) 1.90734863281(Hint: If you get 1, 0 and 1, you should divide by 2.0 instead of 2 to tell Python to use real numbers instead of integers.)
This means if we connected just 20 curves using connect_rigidly, and passed the result to draw_curve_points with one million as the number of points, there would still be only one or two points drawn for the 20th curve. If we are drawing thousands of curves, for most of them, not even a single point would be drawn!
To fix this, we need to distribute the t-values between our curves more fairly. We have provided a procedure connect_curves_evenly in graphics.py that connects a list of curves in a way that distributes the range of t values evenly between the curves.
The definition is a bit complicated, so don't worry if you don't understand it completely. You should, however, be able to figure out the basic idea for how it distributed the t-values evenly between every curve in a list of curves.
def connect_curves_evenly(curvelist):
def new_curve(t):
# We must pick a curve in curvelist to draw for
# this time step t. Which_curve should we draw?
if t >= 1.0:
# Corner case ...
which_curve = len(curvelist)-1
else:
# Some handy Python math:
# int(5.3) == 5
# math.floor(1.2) == 1.0
# math.floor(-1.2) == -2.0
which_curve = int(math.floor(t * len(curvelist)))
# So if there are 5 curves in curvelist and
# we're at t=0.5, we'll draw curve 2.
chosen_curve = curvelist[which_curve]
# In the running example, we'll only draw curve 2
# from t=0.4 to 0.6, so we'll need to stretch
# those points out so that 0.4 to 0.6 becomes
# 0.0 to 1.0.
time = len(curvelist) * \
(t - which_curve * 1.0 / len(curvelist))
# Now just evaluate the chosen curve at the
# given "stretched" time and we're done!
return chosen_curve(time)
return new_curve
It will also be useful to connect curves so that the next curve begins
where the first curve ends. We can do this by translating the second
curve to begin where the first curve ends. To do this for a list of
curves, we translate each curve in the list the same way using map:
def construct_simple_curvelist(curve, curvelist):
endpoint = curve(1.0)
delta_x = x_of_point(endpoint)
delta_y = y_of_point(endpoint)
return [curve] + \
map(lambda thiscurve : translate(thiscurve, delta_x, delta_y), curvelist)
Now that we have defined all of these procedures to manipulate, connect
and draw listscurves, we just have to turn L-System fractals into lists of
curves and then we can draw them!
Drawing L-System Curves
To draw an L-system fractal, we need to convert a sequence of L-system commands into a curve. We defined the connect_curves_evenly procedure to take a list of curves, and produce a single curve that connects all the curves. So, to draw an L-System curve, we need a procedure that turns an L-System Curve into a list of curve procedures.The convert_lcommands_to_curvelist procedure converts a list of L-System commands into a curve. Here is the code for convert_lcommands_to_curvelist (with some missing parts that you will need to complete). It will be explained later, but try to understand it yourself first.
def convert_lcommands_to_curvelist(lcommands):
if len(lcommands) == 0:
# We need to make a leaf with just a single point of green
green = (0,255,0)
return [lambda t:make_colored_point(0,0,green)]
elif is_forward(lcommands[0]):
# Make a vertical_line and then recurse on the rest of the list
return construct_simple_curvelist(vertical_line, \
convert_lcommands_to_curvelist(lcommands[1:]))
elif is_rotate(lcommands[0]):
rotate_angle = -1*get_angle(lcommands[0])
# If this command is a rotate, every curve in the rest
# of the list should be rotated by the rotate angle
# Question 8: fill in this part
return []
elif is_offshoot(lcommands[0]):
# Question 9: fill in this part
return []
else:
# This branch should never happen, but it's good programming
# practice to notice that and raise an error -- "just in
# case".
raise RuntimeError("Bad Command")
We define convert_lcommands_to_curvelist recursively. The base
case is when there are no more commands (the lcommands
parameter is []). It evaluates to the leaf curve (for now, we just
make a point of green — you may want to replace this with
something more interesting to make a better fractal). Since
convert_lcommands_to_curvelist evaluates to a list of
curves, we need to make a singleton list of curves containing only one curve.
Otherwise, we need to do something different depending on what the first command in the command list is. If it is a forward command we draw a vertical line, and connect the rest of the fractal is connected to the end of the vertical line. The recursive call to convert_lcommands_to_curve produces the curve list corresponding to the rest of the L-system commands. Note how we pass (lcommands[1:]) in the recursive call to get the rest of the command list.
You can test your code by drawing the curve that results from any list of L-system commands that does not use offshoots. For example, evaluating
lcommands = make_lsystem_command(make_rotate_command(150), make_forward_command(), make_rotate_command(-120), make_forward_command()) curvelist = convert_lcommands_to_curvelist(lcommands) c1 = connect_curves_evenly(curvelist) c2 = translate(c1, 0.3, 0.7) c3 = position_curve(c2, 0, 0.5) draw_curve_points(c3, 10000)should produce a "V".
Hint 1: See the next few paragraphs for help testing Question 9.
Hint 2: Evaluate tree_commands and look at its definition in graphics.py.
We have provided the position_curve procedure to make it easier to fit fractals into the graphics window:
position_curve(curve, startx, starty) — evaluates to a curve that translates curve to start at (startx, starty) and scales it to fit into the graphics window maintaining the aspect ratio (the x and y dimensions are both scaled the same amount)The code for position_curve is in graphics.py. You don't need to look at it, but should be able to understand it if you want to.
Now, you should be able to draw any l-system command list using position_curve and the convert_lcommands_to_curvelist function you completed in Questions 8 and 9. Try drawing a few simple L-system command lists before moving on to the next part. For example, given this input:
draw_curve_points(position_curve(connect_curves_evenly(convert_lcommands_to_curvelist(tree_commands)), 0.5, 0.1), 5000)Your output should look like this:
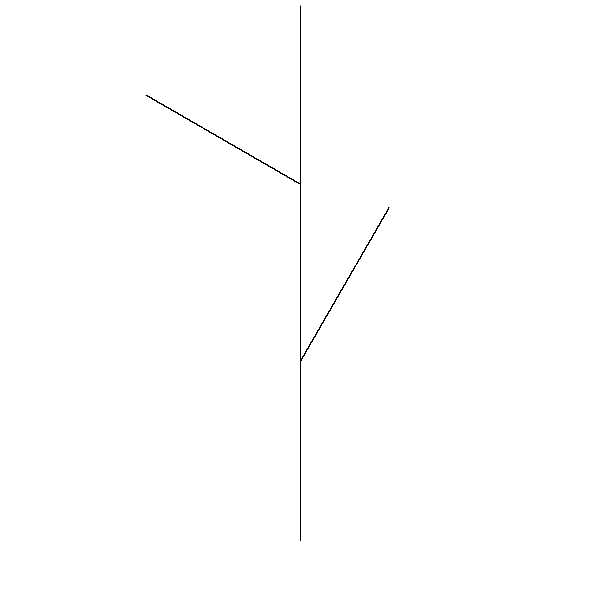
Hint: You should use the rewrite_lcommands you defined in Question 4.
def make_tree_fractal(level):
make_lsystem_fractal(tree_commands, \
make_lsystem_command(make_forward_command), level)
def draw_lsystem_fractal(lcommands):
draw_curve_points(position_curve(connect_curves_evenly( \
convert_lcommands_to_curvelist(lcommands)), 0.5, 0.1), 50000)
For example, draw_lsystem_fractal(make_tree_fractal(3)) will create a tree fractal with 3 levels of branching.
Draw some fractals by playing with the L-system commands. Try changing the rewrite rule, the starting commands, level and leaf curve (in convert_lcommands_to_curvelist) to draw an interesting fractal. You might want to make the branches colorful also (here's that color chart again). Try and make a fractal picture that will make a better course logo than the current Great Lambda Tree Of Infinite Knowledge and Ultimate Power.
Your last-displayed fractal image file is saved in fractal.svg in your current directory. It is over-written every time, so make sure that it looks right before you submit it!
- Please refer to your favorite and least favorite TA by name.
- We will not think less of you (or grade you more harshly later on) for negative comments. The TAs will not see your comments and will only see anonymous summaries.
If you are working with a partner, you should each submit your own answer to this in the version of ps3.py you submit electronically.