Turn-in Checklist:
  1. Bring in to class a stapled turn-in containing your written answers to all the questions by 3:30pm Wednesday, 22 September. If you worked with a partner, you and your partner should submit a single writeup with both of your names and UVA Email Ids on it. You must clearly indicate both names and UVA IDs in big block letters if you are working in a team.
  2. Use our automatic adjudication service to submit a single Scheme file (a modification of ps3.ss) containing all your code answers. You must define an author list. Each partner must separately submit a copy of your joint file. Do this by 3:30pm on Wednesday, 22 September.
  3. Use our automatic adjudication service to submit a single Scheme file and a single PNG file as your answer to Question 12. You must define an author list. Each partner must separately submit copies of the files. For this problem, partners may submit separate fractals if they choose. Do this by 3:30pm on Wednesday, 22 September.
  4. If you are doing the extra credit, email your extra credit Scheme definition file to weimer@cs.virginia.edu by by 3:30pm on Friday, 24 September.

Collaboration Policy - Read Carefully

For this problem set, you may choose to work with a partner of your choice. You are not required to do so.

Before starting to work with a partner, you should go through questions 1 and 2 yourself on paper. When you meet with your partner (if any), check if you made the same predictions. If there are any discrepancies, try to decide which is correct before using DrScheme to evaluate the expressions.

If you have a partner, you and your partner should work together on the rest of the assignment. You should read the whole problem set yourself and think about the questions before beginning to work on them with your partner. Both partners need to understand everything you submit.

Remember to follow the pledge you read and signed at the beginning of the semester. For this assignment, you may consult any outside resources, including books, papers, web sites and people, you wish except for materials from previous cs1120, cs150, and cs200 courses. You may consult an outside person (e.g., another friend who is a CS major but is not in this class) who is not a member of the course staff, but that person cannot type anything in for you and all work must remain your own. That is, you can ask general questions such as "can you explain recursion to me?" or "how do lists work in Scheme?", but outside sources should never give you specific answers to problem set questions. If you use resources other than the class materials, lectures and course staff, explain what you used in your turn-in.

You are strongly encouraged to take advantage of the scheduled help hours and office hours for this course.

Purpose

Download: Download ps3.zip to your machine and unzip it into your home directory J:\cs1120\ps3. This file contains:
  • ps3.ss — A template for your answers. You should do the problem set by editing this file.
  • graphics.ss — Scheme code for drawing curves.
  • lsystem.ss — provided incomplete code for producing L-System Fractals

Warning: Unlike in Problem Set 1 and Problem Set 2, you are expected to be able to understand all the code provided for this problem set (and in all future problem sets in this class unless you are specifically told otherwise). This problem set expects you to write considerably more code than Problem Set 2. We recommend you start early and take advantage of the scheduled help hours.

Background

In this problem set, you will explore a method of creating fractals known as the Lindenmayer system (or L-system). Aristid Lindemayer, a theoretical biologist at the University of Utrecht, developed the L-system in 1968 as a mathematical theory of plant development. In the late 1980s, he collaborated with Przemyslaw Prusinkiewicz, a computer scientist at the University of Regina, to explore computational properties of the L-system and developed many of the ideas on which this problem set is based.

The idea behind L-system fractals is that we can describe a curve as a list of lines and turns, and create new curves by rewriting old curves. Everything in an L-system curve is either a forward line (denoted by F), or a right turn (denoted by Ra where a is an angle in degrees clockwise). We can denote left turns by using negative angles.

We create fractals by recursively replacing all forward lines in a curve list with the original curve list. Lindemayer found that many objects in nature could be described using regularly repeating patterns. For example, the way some tree branches sprout from a trunk can be described using the pattern: F O(R30 F) F O(R-60 F) F. This is interpreted as: the trunk goes up one unit distance, a branch sprouts at an angle 30 degrees to the trunk and grows for one unit. The O means an offshoot — we draw the curve in the following parentheses, and then return to where we started before the offshoot. The trunk grows another unit and now another branch, this time at -60 degrees relative to the trunk grows for one units. Finally the trunk grows for one more unit. The branches continue to sprout in this manner as they get smaller and smaller, and eventually we reach the leaves.

We can describe this process using replacement rules:

Start: (F)
Rule: F ::= (F O(R30 F) F O(R-60 F) F)
Here are the commands this produces after two iterations:
Iteration 0: (F)
Iteration 1: (F O(R30 F) F O(R-60 F) F)
Iteration 2: (F O(R30 F) F O(R-60 F) F O(R30 F O(R30 F) F O(R-60 F) F) F O(R30 F) F O(R-60 F) F O(R-60 F O(R30 F) F O(R-60 F) F) F O(R30 F) F O(R-60 F) F)

[Correction Added 21 September] The originally-posted version of this problem set included example images that make the rotates in the wrong direction. The example images below have been corrected to match the description in the problem set. A Ra command should rotate right (clockwise) by a degrees, as described above, and shown in the revised images below. Sorry for the confusion! (Thanks to Richard McPherson for noticing this.)
Here's what that looks like:

Iteration 0
Iteration 1

Iteration 2
Iteration 5

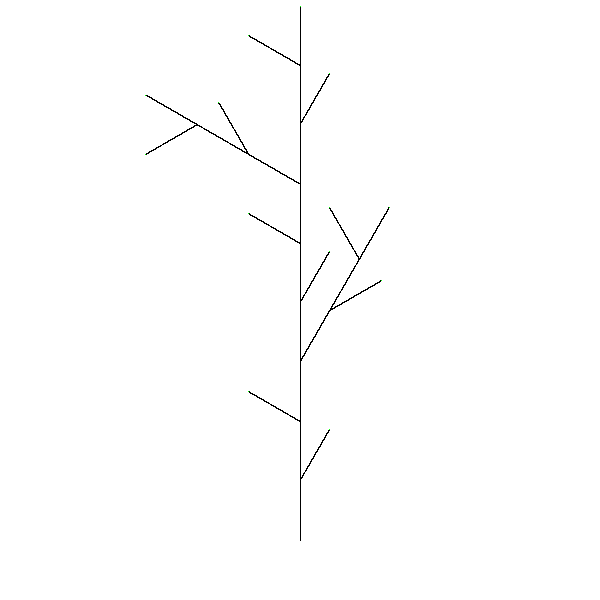
Iteration 5 (with color)
The Great Lambda Tree of
Infinite Knowledge and Ultimate Power

Note that L-system command rewriting is similar to the replacement rules in a BNF grammar. The important difference is that with L-system rewriting, each iteration replaces all instances of F in the initial string instead of just picking one to replace.

We can divide the problem of producing an L-system fractal into two main parts:

  1. Produce a list of L-system commands that represents the fractal by rewriting according to the L-system rule; and
  2. Drawing a list of L-system commands.
We will first work on producing the list of L-system commands, and then work on how to draw a list of L-system commands.

Representing L-System Commands

Here is a BNF grammar for L-system commands:

  1. CommandSequence ::= ( CommandList )
  2. CommandList ::= Command CommandList
  3. CommandList ::=
  4. Command ::= F
  5. Command ::= RAngle
  6. Command ::= OCommandSequence
  7. Angle ::= Number

Question 1: Show that (F O(R-60 F) F) is a string in the language defined by our BNF grammar. To do this, you should start with CommandSequence, and show a sequence of replacements that follow the grammar rules that produce the target string. You can use the rule numbers above to identify the rules.

We need to find a way to turn strings in this grammar into objects we can manipulate in a Scheme program. We can do this by looking at the BNF grammar, and converting the non-terminals into Scheme objects. 

;;; CommandSequence ::= ( CommandList )
(define make-lsystem-command list)

;;; We represent the different commands as pairs where the first item in the
;;; pair is a tag that indicates the type of command: 'f for forward, 'r for
;;; rotate and 'o for offshoot.  We use quoted letters to make tags, which 
;;; evaluate to the quoted letter.  The tag 'f is short for (quote f).

;;; Command ::= F
(define (make-forward-command) (cons 'f #f)) ;; No value, just use false.

;;; Command ::= RAngle
(define (make-rotate-command angle) (cons 'r angle))

;;; Command ::= OCommandSequence
(define (make-offshoot-command commandsequence) (cons 'o commandsequence))

Question 2: It will be useful to have procedures that take L-system commands as parameters, and return information about those commands. Define the following procedures in ps3.ss:
  • (is-forward? lcommand) — evaluates to #t if the parameter passed is a forward command (indicated by its first element being a 'f tag).
  • (is-rotate? lcommand)
  • (is-offshoot? lcommand)
  • (get-angle lcommand) — evaluates to the angle associated with a rotate command. Produces an error if the command is not a rotate command (see below for how to produce an error).
  • (get-offshoot-commands lcommand) — evaluates to the offshoot command list associated with an offshoot command. Produces an error if the command is not an offshoot command.

You will find the following procedures useful:

If you define these procedures correctly, you should produce these evaluations:

> (is-forward? (make-forward-command))

#t

> (is-forward? (make-rotate-command 90))

#f

> (get-angle (make-rotate-command 90))

90

> (get-angle (make-forward-command))

Yikes! Attempt to get-angle for a command that is not an angle command

You should be able to make up similar test cases yourself to make sure the other procedures you defined work.

New Special Forms

The code for this problem set uses three special forms that were not included in our original Scheme language description. None of the new special forms are necessary for expressing these programs — they could easily be rewritten using just the subset of Scheme introduced in Chapter 3 — but, as our programs get more complex it will be useful to use these expressions to make our programs shorter and clearer.

Begin Expression

The grammar rule for begin is:
Expression ::= BeginExpression
BeginExpression ::= (begin MoreExpressions Expression)
The evaluation rule for begin is:
Evaluation Rule 6: Begin. To evaluate (begin Expression1 Expression2 ... Expressionk), evaluate each sub-expression in order from left to right. The value of the begin expression is the value of Expressionk.
The begin special form is useful when we are evaluating expressions that have side-effects. This means the expression is important not for the value it produces (since the begin expression ignores the values of all expressions except the last one), but for some change to the state of the machine it causes.

The special define syntax for procedures includes a hidden begin expression. The syntax, 

   (define (Name Parameters) 
       MoreExpressions Expression)
is an abbreviation for: 
   (define name
       (lambda (Parameters) 
          (begin MoreExpressions Expression)))

Let Expression

The grammar rule for let expressions is:
Expression ::= LetExpression
LetExpression ::= (let (Bindings) Body)
Body ::= MoreExpressions Expression
Bindings ::= Binding Bindings
Bindings ::=
Binding ::= (Name Expression)
The evaluation rule for a let expression is:
Evaluation Rule 7: Let. To evaluate a let expression, evaluate each binding in order. To evaluate each binding, evaluate the binding expression and bind the name to the value of that expression. Then, evaluate the body expressions in order with the names in the expression that match binding names substituted with their bound values. The value of the let expression is the value of the last body expression.
A let expression can be transformed into an equivalent application expression. The let expression 
(let ((Name1 Expression1) 
      (Name2 Expression2) 
      ...
      (Namek Expressionk))
    MoreExpressions Expression)
is equivalent to the application expression: 
((lambda (Name1 
          Name2
          ... 
          Namek)
    (begin MoreExpressions Expression))
 Expression1 
 Expression2
 ... 
 Expressionk)
The advantage of the let expression syntax is it puts the expressions next to the names to which they are bound. For example, the let expression: 
  (let ((a 2)
        (b (* 3 3)))
    (+ a b))
is easier to understand than the corresponding application expression: 
   ((lambda (a b) (+ a b)) 2 (* 3 3))

Conditional Expression

Conditional expressions provide a way to concisely combine many decisions. The grammar rule for cond is:
Expression ::= CondExpression
CondExpression ::= (cond ClauseList)
ClauseList ::=
ClauseList ::= Clause ClauseList
Clause ::= (ExpressionTest ExpressionAction)
Clause ::= (else ExpressionAction)
The evaluation rule is:
Evaluation Rule 8: Conditionals. To evaluate a CondExpression, evaluate each clause's test expression in order until one is found that evaluates to a true value. Then, evaluate the action expression of that clause. The value of the CondExpression is the value of the action expression. If none of the test expressions evaluate to a true value, if the CondExpression includes an else clause, the value of the CondExpression is the value of the action expression associated with the else clause. If none of the test expressions evaluate to a true value, and the CondExpression has no else clause, the CondExpression has no value.
Note that a conditional expression could straightforwardly be translated into an equivalent if expression: 
   (cond (Test1 Action1)
         (Test2 Action2)
         ...
	 (Testk Actionk)
         (else Actionelse))
is equivalent to: 
   (if Test1 Action1
       (if Test2 Action2
           ...
               (if Testk Actionk
                   actionelse)...))
Question 3: Demonstrate how any if expression can be rewritten as an equivalent conditional expression. A convincing demonstration would include a transformation similar to the one we showed for transforming a conditional expression into an equivalent if expression, but that transforms an if expression into the equivalent cond expression.

Question 4: Is the begin expression necessary? Either explain how to obtain the same exact behavior as (begin Expr1 Expr2) without using begin, or explain why it is not possible to obtain the same behavior using only the subset of Scheme defined in Chapter 3.

Rewriting Curves

The power of the L-System commands comes from the rewriting mechanism. Recall how we described the tree fractal:
Start: (F)
Rule: F ::= (F O(R30 F) F O(R-60 F) F)
To produce levels of the tree fractal, we need a procedure that takes a list of L-system commands and replaces each F command with the list of L-system commands given by the rule.

So, for every command in the list:

One slight complication is that the replacement commands are a list of L-system commands, and we want to end up with a flat list of L-System commands.

For example, consider a simple L-System rewriting:

Start: (F)
Rule: F ::= (F R30 F)
We want to get:
Iteration1: (F R30 F)
Iteration2: (F R30 F R30 F R30 F)
but if we just replace F's with (F R30 F) lists, we would get:
Iteration1: ((F R30 F))
Iteration2: ((F R30 F) R30 (F R30 F))
The easiest way to fix this problem is to flatten the result. The code should look similar to many recursive list procedures you have seen (this code is provided in lsystem.ss): 
(define (flatten-commands ll)
  (if (null? ll) ll
      (if (is-lsystem-command? (car ll))
	  (cons (car ll) (flatten-commands (cdr ll)))
	  (flat-append (car ll) (flatten-commands (cdr ll))))))

(define (flat-append lst ll)
  (if (null? lst) ll
      (cons (car lst) (flat-append (cdr lst) ll))))

Question 5: Define a procedure rewrite-lcommands in ps3.ss that takes a list of L-system commands as its first parameter. The second parameter is a list of L-system commands that should replace every forward command in the first list of commands in the result.

Here's the easy part: 

(define (rewrite-lcommands lcommands replacement)
  (flatten-commands
   (map 
   ; Procedure to apply to each command
   lcommands)))
Complete the definition of rewrite-lcommands.

We have pre-defined some simple lsystem commands (e.g., f, f-r30-f, f-f-r30) for easy testing. If you define these procedures correctly, you should produce these evaluations:

> (rewrite-lcommands f f-r30-f)

((f . #f) (r . 30) (f . #f))

> (rewrite-lcommands f-r30-f f-f-r30)

((f . #f) (f . #f) (r . 30) (r . 30) (f . #f) (f . #f) (r . 30))

To make interesting L-system curves, we will need to apply rewrite-lcommands many times. We will leave that until the last question. Next, we will work on turning sequences of L-system commands into curves we can draw.

Drawing L-System Fractals

To draw our L-system fractals, we will need procedures for drawing curves. There are many of different ways of thinking about curves. Mathematicians sometimes think about curves as functions from an x coordinate value to a y coordinate value. The problem with this way of thinking about curves is there can only be one y point for a given x point. This makes it impossible to make simple curves like a circle where there are two y points for every x value on the curve. So, a more useful way of thinking about curves is as functions from a number to a point. We can produce infinitely many different points on the curve by evaluating the curve function with the (infinitely many different) real numbers between 0 and 1 inclusive. Of course, we can't really evaluate the curve function at every value between 0 and 1. Instead, we will evaluate it at a large number of points distributed between 0 and 1 to display an approximation of the curve.

Points

We need a way to represent the points on our curves. A point is a pair of two values, x and y representing the horizontal and vertical location of the point.

We will use a coordinate system from (0, 0) to (1, 1):

(0.0, 1.0) (1.0, 1.0)
(0.0, 0.0) (1.0, 0.0)

Points have x and y coordinates. To represent points we would like to define procedures make-point, x-of-point and y-of-point. Our pictures will be more interesting if points can have color too. So, we represent a colored point using a list of three values: x, y and color: 

(define (make-point x y) (list x y))
(define (make-colored-point x y c) (list x y c))
(define (is-colored-point? (= (length point) 3)

(define (x-of-point point) (car point))
(define (y-of-point point) (cadr point)) ;; (cadr x) = (car (cdr x))

;;; Regular points are black.  Colored points have a color.
(define (color-of-point point)
  (if (is-colored-point? point)
      (caddr point) ;; == (car (cdr (cdr point)))
      (make-color 0 0 0)))
Note that we have defined points so we can have both colored points and colorless points that appear black.

We have provided some procedures for drawing on the window in graphics.ss:

Read through graphics.ss and look for other handy functions.

Drawing Curves

Building upon points, we can make curves and lines (straight lines are just a special kind of curve). Curves are procedures from values to points. One way to represent a curve is as a procedure that evaluates to a point for every value between 0.0 and 1.0. For example, 
   (define (mid-line t)
      (make-point t 0.5))
defines a curve that is a horizontal line across the middle of the window. If we apply mid-line to a value x, we get the point (x, 0.5). Hence, if we apply mid-line to all values between 0.0 and 1.0, we get a horizontal line.

Predict what (x-of-point (mid-line 0.7)) and (y-of-point (mid-line 0.7)) should evaluate to. Try them in your Interactions window.

Of course, there are infinitely many values between 0.0 and 1.0, so we can't apply the curve function to all of them. Instead, we select enough values to show the curve well. To draw a curve, we need to apply the curve procedure to many values in the range from 0.0 to 1.0 and draw each point it evaluates to. Here's a procedure that does that: 

  (define (draw-curve-points curve n)
    (define (draw-curve-worker curve t step)
      (if (<= t 1.0)
	   (begin
	     (window-draw-point (curve t))
	     (draw-curve-worker curve (+ t step) step))))
    (draw-curve-worker curve 0.0 (/ 1 n)))
The procedure draw-curve-points takes a procedure representing a curve, and n, the number of points to draw. It calls the draw-curve-worker procedure. The draw-curve-worker procedure takes three parameters: a curve, the current time step values, and the difference between time step values. Hence, to start drawing the curve, draw-curve-points evaluates draw-curve-worked with parameters curve (to pass the same curve that was passed to draw-curve-points), 0.0 (to start at the first t value), and (/ 1 n) (to divide the time values into n steps).

The draw-curve-worker procedure is defined recursively: if t is less than or equal to 1.0, we draw the current point using (window-draw-point (curve t)) and draw the rest of the points by evaluating (draw-curve-worker curve (+ t step) step)).

We stop once t is greater than 1.0, since we defined the curve over the interval [0.0, 1.0].

The draw-curve-worker code uses a being expression. The first expression in the begin expression is (window-draw-point (curve t)). The value it evaluates to is not important, what matters is the process of evaluating this expression draws a point on the display.

Question 6:
  1. Define a procedure, vertical-mid-line that can be passed to draw-curve-points so that (draw-curve-points vertical-mid-line 1000) produces a vertical line in the middle of the window.

  2. Define a procedure, make-vertical-line that takes one parameter and produces a procedure that produces a vertical line at that horizontal location. For example, (draw-curve-points (make-vertical-line 0.5) 1000) should produce a vertical line in the middle of the window and (draw-curve-points (make-vertical-line 0.2) 1000) should produce a vertical line near the left side of the window.

Hint: Need to clear your window to practice and test things out? Since you've already read graphics.ss, you should skim it again for (clear-window). You could also just re-run or re-execute your Scheme definitions (press ctrl-t).

Manipulating Curves

The good thing about defining curves as procedures is it is easy to modify and combine then in interesting ways.

For example, the procedure rotate-ccw takes a curve and rotates it 90 degrees counter-clockwise by swapping the x and y points: 

(define (rotate-ccw curve)
  (lambda (t)
    (let ((ct (curve t)))
      (make-colored-point
       (- (y-of-point ct)) (x-of-point ct)
       (color-of-point ct)))))
We use a let expression here to avoid needing to evaluate (curve t) more than once. It binds the value (curve t) evaluates to, to the name ct.

Note the use of (- (y-of-point ct)). In Scheme, (- 27) evaluates to -27, the same result as (- 0 27).

Note that (rotate-ccw c) evaluates to a curve. The function rotate-ccw is a procedure that takes a procedure (a curve) and returns a procedure that is a curve.

Predict what (draw-curve-points (rotate-ccw mid-line) 1000) and (draw-curve-points (rotate-ccw (rotate-ccw mid-line)) 1000) will do. Confirm your predictions by trying them in your Interactions window.

Here's another example: 

(define (shrink curve scale)
  (lambda (t)
    (let ((ct (curve t)))
      (make-colored-point
       (* scale (x-of-point ct))
       (* scale (y-of-point ct))
       (color-of-point ct)))))
Predict what (draw-curve-points (shrink mid-line .5) 1000) will do, and then try it in your Interactions window.

The shrink procedure doesn't produce quite what we want because in addition to changing the size of the curve, it moves it around. Why does this happen? Try shrinking a few different curves to make sure you understand why the curve moves.

One way to fix this problem is to center our curves around (0,0) and then translate them to the middle of the screen. We can do this by adding or subtracting constants to the points they produce: 

(define (translate curve x y)
  (lambda (t)
    (let ((ct (curve t)))
      (make-colored-point
       (+ x (x-of-point ct)) (+ y (y-of-point ct))
       (color-of-point ct)))))
Now we have translate, it makes more sense to define mid-line this way: 
   (define (horiz-line t) (make-point t 0))
   (define mid-line (translate horiz-line 0 0.5))
Question 7: To check you understand everything so far, define a procedure half-line that uses translate, horiz-line and shrink to draw a line half the width of the window that starts in the middle of the display window.

When you are done, (draw-curve-points half-line 1000) should produce a horizontal line that starts in the middle of the window and extends to the right boundary.

Hint: If you do not see anything when you are drawing a curve, it may be that you haven't yet applied translate and the points are being drawn along the bottom edge of the screen.

In addition to altering the points a curve produces, we can alter a curve by changing the t values it will see. For example, 

(define (first-half curve)
   (lambda (t) (curve (/ t 2))))
is a function that takes a curve and produces a new curve that is just the first half of the passed curve.

Predict what each of these expressions will do:

Try evaluating them in your Interactions window to check if you were right. (Remember to use (clear-window) to clear the display window so you can see the new curve without the old one.)

The provided code includes several other functions that transform curves including:

You should be able to understand the code in graphics.ss that defines these functions.

It is also useful to have curve transforms where curves may be combined. An example is (connect-rigidly curve1 curve2) which evaluates to a curve that consists of curve1 followed by curve2. The starting point of the new curve is the starting point of curve1 and the end point of curve2 is the ending point of the new curve. Here's how connect-rigidly is defined: 

(define (connect-rigidly curve1 curve2)
    (lambda (t)
      (if (< t (/ 1 2))
          (curve1 (* 2 t))
          (curve2 (- (* 2 t) 1)))))
Predict what (draw-curve-points (connect-rigidly vertical-mid-line mid-line) 1000) will do. Is there any difference between that and (draw-curve-points (connect-rigidly mid-line vertical-mid-line) 1000)? Check your predictions in the Interactions window.

Distributing t Values

The draw-curve-points procedure does not distribute the t-values evenly among connected curves, so the later curves appear dotty. This isn't too big a problem when only a few curves are combined; we can just increase the number of points passed to draw-curve-points to have enough points to make a smooth curve. In this problem set, however, you will be drawing curves made up of thousands of connected curves. Just increasing the number of points won't help much, as you'll see in Question 8.

The way connect-rigidly is defined above, we use all the t-values below 0.5 on the first curve, and use the t-values between 0.5 and 1.0 on the second curve. If the second curve is the result of connecting two other curves, like (connect-rigidly c1 (connect-rigidly c2 c3)) then 50% of the points will be used to draw c1, 25% to draw c2 and 25% to draw c3.

Question 8: Define a procedure num-points that determines the approximate number of t-values that will be used for the nth curve when drawing 
   (connect-rigidly c1 (connect-rigidly c2 (connect-rigidly curve3 (... cn))))
The first argument to num-points is the number of t-values left. The second argument is the number of curves left.

Think about this yourself first, but look in ps3.ss for a hint if you are stuck. There are mathematical ways to calculate this efficiently, but the simplest way to calculate it is to define a procedure that keeps halving the number of points n times to find out how many are left for the nth curve.

Your num-points procedure should produce results similar to:

> (exact->inexact (num-points 1000 10))

1.953125

> (exact->inexact (num-points 1000 20))

0.0019073486328125

> (exact->inexact (num-points 1000000 20))

1.9073486328125

This means if we connected just 20 curves using connect-rigidly, and passed the result to draw-curve-points with one million as the number of points, there would still be only one or two points drawn for the 20th curve. If we are drawing thousands of curves, for most of them, not even a single point would be drawn!

To fix this, we need to distribute the t-values between our curves more fairly. We have provided a procedure connect-curves-evenly in graphics.ss that connects a list of curves in a way that distributes the range of t values evenly between the curves.

The definition is a bit complicated, so don't worry if you don't understand it completely. You should, however, be able to figure out the basic idea for how it distributed the t-values evenly between every curve in a list of curves. 

(define (connect-curves-evenly curvelist)
  (lambda (t)
    (let ((which-curve
	   (if (>= t 1.0) (- (length curvelist) 1)
	       (inexact->exact (floor (* t (length curvelist)))))))
      ((get-nth curvelist which-curve)
       (* (length curvelist)
	  (- t (* (/ 1 (length curvelist)) which-curve)))))))
It will also be useful to connect curves so that the next curve begins where the first curve ends. We can do this by translating the second curve to begin where the first curve ends. To do this for a list of curves, we translate each curve in the list the same way using map: 
(define (cons-to-curvelist curve curvelist)
  (let ((endpoint (curve 1.0))) ;; The last point in curve
    (cons curve
	  (map (lambda (thiscurve)
		 (translate thiscurve 
                            (x-of-point endpoint) (y-of-point endpoint)))
	       curvelist))))

Drawing L-System Curves

To draw an L-system curve, we need to convert a sequence of L-system commands into a curve. We defined the connect-curves-evenly procedure to take a list of curves, and produce a single curve that connects all the curves. So, to draw an L-System curve, we need a procedure that turns an L-System Curve into a list of curve procedures.

The convert-lcommands-to-curvelist procedure converts a list of L-System commands into a curve. Here is the code for convert-lcommands-to-curvelist (with some missing parts that you will need to complete). It will be explained later, but try to understand it yourself first. 

(define (convert-lcommands-to-curvelist lcommands)
  (cond ((null? lcommands)
	 (list 
	  ;;; We make a leaf with just a single point of green:
	  (lambda (t) 
	    (make-colored-point 0.0 0.0 (make-color 0 255 0))) 
	  ))
	((is-forward? (car lcommands))
	 (cons-to-curvelist
	  vertical-line
	  (convert-lcommands-to-curvelist (cdr lcommands))))
	((is-rotate? (car lcommands))
	      ;;; If this command is a rotate, every curve in the rest 
	      ;;; of the list should should be rotated by the rotate angle
	 (let
	     ;; L-system turns are clockwise, so we need to use - angle
	     ((rotate-angle (- (get-angle (car lcommands)))))
	   (map
	    (lambda (curve)
              ;;; Question 9: fill this in
	      )
	     ;;; Question 9: fill this in
	    )))
	((is-offshoot? (car lcommands))
	 (append
  	  ;;; Question 10: fill this in
	  ))
	(#t (error "Bad lcommand!"))))
We define convert-lcommands-to-curvelist recursively. The base case is when there are no more commands (the lcommands parameter is null). It evaluates to the leaf curve (for now, we just make a point of green — you may want to replace this with something more interesting to make a better fractal). Since convert-lcommands-to-curvelist evaluates to a list of curves, we need to make a list of curves containing only one curve.

Otherwise, we need to do something different depending on what the first command in the command list is. If it is a forward command we draw a vertical line. The rest of the fractal is connected to the end of the vertical line using cons-to-curvelist. The recursive call to convert-lcommands-to-curve produces the curve list corresponding to the rest of the L-system commands. Note how we pass (cdr lcommands) in the recursive call to get the rest of the command list.

Question 9: Fill in the missing code for handling rotate commands (marked as Question 9 in ps3.ss). You will want to use (rotate-around-origin curve rotate-angle) somewhere in your code to rotate every curve after the rotate command by the rotate-angle.

You can test your code by drawing the curve that results from any list of L-system commands that does not use offshoots. For example, evaluating 

(draw-curve-points
   (position-curve
    (translate
     (connect-curves-evenly
      (convert-lcommands-to-curvelist
       (make-lsystem-command (make-rotate-command 150)
                             (make-forward-command)
                             (make-rotate-command -120)
                             (make-forward-command))))
     0.3 0.7)
    0 .5)
   10000)
should produce a "V".

Question 10: Fill in the missing code for handling offshoot commands (marked as Question 10 in ps3.ss).

Hint 1: See the next few paragraphs for help testing Question 10.

Hint 2: Evaluate tree-commands and look at its definition in lsystem.ss. This may help you to visualize relevant car and cdr combinations.

We have provided the position-curve procedure to make it easier to fit fractals into the graphics window:

(position-curve curve startx starty) — evaluates to a curve that translates curve to start at (startx, starty) and scales it to fit into the graphics window maintaining the aspect ratio (the x and y dimensions are both scaled the same amount)
The code for position-curve is in curve.ss. You don't need to look at it, but should be able to understand it if you want to.

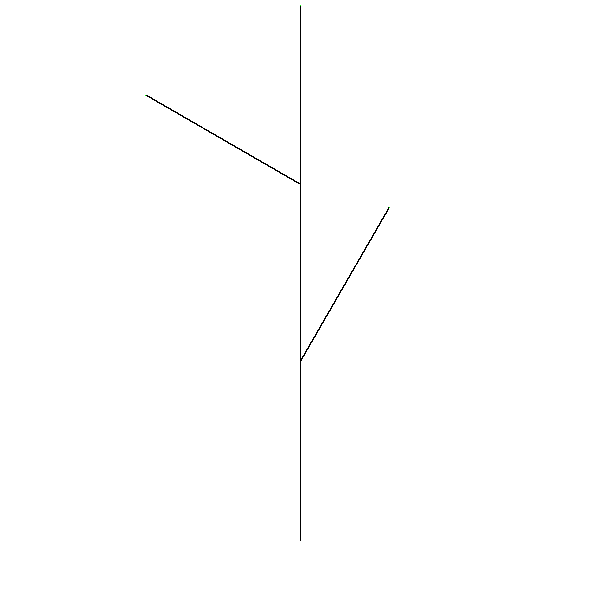
Now, you should be able to draw any l-system command list using position-curve and the convert-lcommands-to-curvelist function you completed in Questions 9 and 10. Try drawing a few simple L-system command lists before moving on to the next part. For example, given this input: 

(draw-curve-points
 (position-curve
  (connect-curves-evenly
   (convert-lcommands-to-curvelist tree-commands))
  0.5 0.1)
 50000)
Your output should look like this:

Question 11: Define a procedure make-lsystem-fractal in ps3.ss that takes three parameters: replace-commands, a list of L-system commands that replace forward commands in the rewriting; start, a list of L-system commands that describes the starting curve; level, the number of iterations to apply the rewrite rule.

Hint: You should use the rewrite-lcommands you defined in Question 5. You may also find it useful to use the n-times function (which we may have described in lecture): 

(define (n-times proc n)
  (if (= n 1) proc
        (compose proc (n-times proc (- n 1)))))
You should be able to draw a tree fractal using make-tree-fractal and draw-lsystem-fractal (these and the tree-commands list of L-system commands are defined in lsystem.ss): 

(define (make-tree-fractal level)
  (make-lsystem-fractal tree-commands 
			(make-lsystem-command (make-forward-command)) level))

(define (draw-lsystem-fractal lcommands)
  (draw-curve-points 
   (position-curve 
    (connect-curves-evenly (convert-lcommands-to-curvelist lcommands)) 
    0.5 0.1) 
   50000))

For example, (draw-lsystem-fractal (make-tree-fractal 3)) will create a tree fractal with 3 levels of branching.

Draw some fractals by playing with the L-system commands. Try changing the rewrite rule, the starting commands, level and leaf curve (in convert-lcommands-to-curvelist) to draw an interesting fractal. You might want to make the branches colorful also. Try an make a fractal picture that will make a better course logo than the current Great Lambda Tree Of Infinite Knowledge and Ultimate Power.

To save your fractal in an image file, use the save-image procedure (defined in lsystem.ss). It can save images as .png files. For example, to save your fractal as yggdrasil.png evaluate 

(save-image "yggdrasil.png")
(Yggradsil is just an example, like "foo" or "jane doe". Pick whatever name you like.) Especially ambitious students may find the Viewport Graphics documentation useful for enhancing your pictures.

Question 12: Submit your best fractal image and the code you used to create it. Note that you may only submit "raw" images created with Scheme -- no altering things up with Photoshop. We encourage you to be as creative as possible. Note that you can use draw-lsystem-fractal (etc.), just modify things to make a "new-looking" image. If your image is interesting or beautiful enough, you may receive untold fame and eternal glory by having it be used as the course logo.
Question 13: Define a variable ta-comments that is a string containing your thoughts on your interactions with the TAs. Your string may contain line breaks if you like, or it can be one long line. Your answers will help me determine who is hired as a TA in future semesters, and may influence my letters of recommendation for current TAs.
  • Please refer to your favorite and least favorite TA by name.
  • We will not think less of you (or grade you more harshly later on) for negative comments. The TAs will not see your comments and will only see anonymous summaries.
You will receive full credit for this question for any comment longer than 40 characters, but we appreciate more helpful comments.

If you are working with a partner, you should each submit your own answer to this in the version of ps3.ss you submit electronically.

Submission: Submit electronically a single Scheme Definition file including all of your code. Your scheme file should be a modification of the ps3.ss file. Each partner must submit the file separately. In addition, each partner should submit an image and code for Question 12. Bring in to class a stapled turn-in containing your written answers to all the questions by the due date. If you worked with a partner, you and your partner should submit a signle writeup with both of your names and UVA Email Ids on it.

(Everything below here is extra credit only.)

Extra Credit: Cognitive Psychology and Mental Rotation

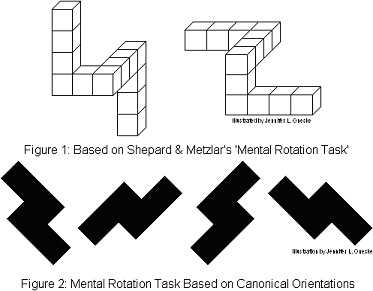One of the great success stories in cognitive psychology is the study of mental rotation — how humans rotate mental representations of objects. If you consider the figures on the right, with a bit of reasoning you should be able to confirm that you could rotate the leftmost image in Figure 2 to form the second image in Figure 2 but not the third image in Figure 2. To get from the first image to the third image, you'd need to flip or mirror it. As a more complicated example, the leftmost three-dimensional image in Figure 1 cannot be rotated in space to form the rightmost image — but this should take you longer to verify. (If you're not quite certain what we mean by rotating a three-dimensional image in space, click here for an animation.)

Cognitive psychologists, such as Roger Shepard and Jacqueline Metzler, have been interested in studying how humans manipulate mental representations of objects. To study this, they conducted a scientific experiment with a falsifiable hypothesis. In essence, their main hypothesis was that the time required to recognize that two perspective drawings portray objects of the same three-dimensional shape is found to be a linearly increasing function of the angular difference in the portrayed orientations of the two objects. To test this hypothesis, they presented subjects with a series of image pairs. Each pair of images was either one drawing and its rotation (as in Figure 2), or one drawing and another drawing that cannot be obtained from it by rotation (as in Figure 1). They then measured the time it took for human subjects to determine whether or not the two shapes were equivalent modulo rotation.

It turns out that the number of seconds it takes humans to determine if the images are rotations or not is a linear function of the angle of rotation. For example, if the angle is 40 degrees, it takes 2 seconds. If the angle is 60 degrees, it takes 3 seconds. If the angle is 80 degrees, it takes 4 seconds. In this example, it takes one second to reason about a 20 degree rotation.

There are many tasks in perception that take constant time. For example, detecting a red X against a random pattern of blue Os takes constant time, regardless of how many Os are present. Some aspects of perception are thus handled in parallel. The "linear function" result for mental rotation suggested that humans actually form a mental model of the object and rotate that model internally to see if it matches up with the other image. Subsequent experimentation with nuclear magnetic resonance and functional magnetic resonance imaging showed that there are particular areas of the brain associated with such mental rotation. Moreover, when a subject is performing a mental rotation tasks, mappings of which neurons are firing for shapes that themselves rotate over time.

This extra credit assignment involves reproducing parts of the original mental rotation experiment. The first part is to read Shepard and Metzler's Mental Rotation of Three-Dimensional Objects from Science volume 701, February 1971. It's only three pages long.

Eventually we will have datapoints from human subjects: rotational angles and the time taken to perform the task. We will want to analyze those datapoints to determine the slop of the line (as in Figure 2 of Shepard and Metzler's article). Write a function calculate-slope that takes a single argument: a list of datapoints. Each datapoint is a cons cell containing a rotation angle measurement and a time value measurement. Your function should return the average slope (rotation/time) for all of the datapoints.

For example:

(define dataset (list (cons 32 1) (cons 54 2) (cons 95 3)))

(calculate-slope dataset)

30 2/9

In that dataset, it takes one second to reason about a 30.16 degree rotation.

We'll also need some way of getting timed user input. We'll assume a function get-timed-input that asks the user for a string and returns a pair containing the time taken and the string. You need not be able to write such a function, but you should be able to understand it: 

(define (get-timed-input)
  (let ((start-time (current-milliseconds)) 
        (input (read-line (current-input-port)))
        (end-time (current-milliseconds)))
        (cons (- end-time start-time) input)))

(get-timed-input)

y
(498 . "y")

(get-timed-input)

n
(651 . "n")

(get-timed-input)

y
(322 . "y")

The basic idea of the experiment is to present the user with a series of image pairs and record the times and answers. We'll use the following image: 
(define (mr-curve degrees)
  (connect-curves-evenly (convert-lcommands-to-curvelist 
  (make-lsystem-command
   (make-rotate-command degrees)
   (make-forward-command) (make-forward-command) (make-forward-command)   
   (make-rotate-command 90)  (make-forward-command)
   (make-rotate-command -90) (make-forward-command)
   (make-rotate-command -90) (make-forward-command) (make-forward-command)
   (make-rotate-command 90)  (make-forward-command)
   (make-rotate-command 90)  (make-forward-command) (make-forward-command) (make-forward-command)
   (make-rotate-command 90)  (make-forward-command) (make-forward-command) (make-forward-command)
   (make-rotate-command 90)  (make-forward-command)
   (make-rotate-command -90) (make-forward-command) (make-forward-command)
   (make-rotate-command 90)  (make-forward-command)   
))))
Define a procedure run-mr-experiment that accepts a single parameter. That parameter is a list of cons cells. Each cons cell holds an angle in degrees and a boolean — the boolean is #t if the image should be flipped before being displayed. For each item in the list, you should clear the screen, display (mr-curve 0) on the left side of the screen, and display a rotated-and-possibly-flipped version of mr-curve on the right side of the screen based on the current list element. The user should enter "y" if it is a rotation and "n" if it is not (i.e., if a flip was involved). You should gather all of the times for which the user was correct as a dataset -- a list suitable for passing to (calculate-slope).

Hint: you may need to write your own version of position-curve to make this work.

Extra Credit Submission: To submit the extra credit, email your Scheme definition file to weimer@cs.virginia.edu with subject "PS3 Extra Credit".

Credits: This problem set was originally created for CS200 Spring 2002 by Dante Guanlao, Jon Erdman and David Evans, and revised for CS200 Spring 2003 by Jacques Fournier and David Evans, and revised for CS200 Spring 2004, CS150 Fall 2005, and CS150 Spring 2007 by David Evans. A version of this assignment was also used at the University of Georgia. Most recently, it was modified for CS 150 in Spring 2009 by Westley Weimer (including adding the Extra Credit section), and updated for cs1120 Fall 2009 by David Evans.