Adaptive Blocks: A High Performance Data Structure

Abstract:

We examine a data structure which uses flexible "adaptivity" to obtain high performance for both serial and parallel computers. The data structure is an adaptive grid which partitions a given region into regular cells. Its closest relatives are cell-based tree decompositions, but there are several important differences which lead to significant performance advantages. Using this block data structure to support adaptive mesh refinement (AMR), we were able to sustain 17 GFLOPS in ideal magnetohydrodynamic (MHD) simulations of the solar wind emanating from the base of the solar corona, using a 512 processor Cray T3D at NASA Goddard.

Keywords:

adaptive mesh refinement (AMR), spatial decomposition, adaptive blocks, quadtree, octree, dynamic data structure, high performance computing, parallel computing, magnetohydrodynamics (MHD)

Introduction

However, there is overhead associated with AMR, in terms of deciding when and how to adapt, and in keeping track of the evolving mesh. One data structure which has been used for AMR is the cell-based tree, which is very flexible and provides a systematic way to keep track of the mesh. However, since each node of a cell-based tree data structure is a single cell, computations suffer from significant overhead due to indirect addressing and lower FLOP rates are achieved. Similar performance issues arise when general unstructured grids are used in place of tree data structures.

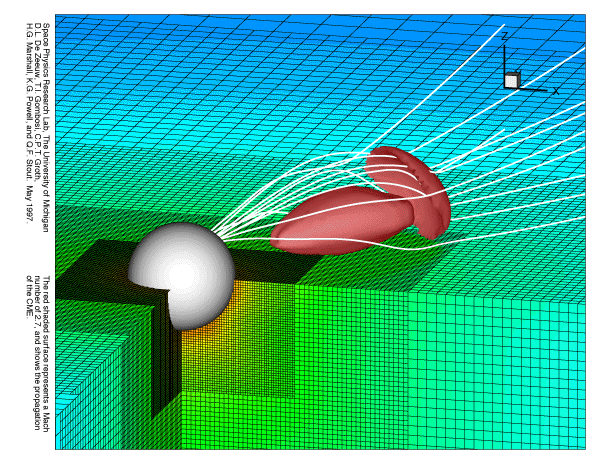
For improved computational performance, we have developed adaptive blocks as an alternative data structure to overcome the disadvantages of cell-based trees and unstructured meshes, while still permitting flexible AMR. Adaptive blocks are particularly well suited to high-performance machines, both serial and parallel. For example, our NASA Grand Challenge Team has made use of this data structure in ideal MHD simulations of the solar wind and inner heliosphere ([2]), achieving 16 GFLOPS performance on a 512 node Cray T3D. Figure 1 shows the results of a coronal mass ejection (CME) simulation obtained using the block adaptive MHD model. An adaptive block structure was also used in the first accurate numerical modeling of the recently observed x-ray emissions from comets ([3]),, where these calculations were performed on a workstation.. Other applications and illustrations can be found at our group's web site, http://hpcc.engin.umich.edu/HPCC/. The web site also provides pointers to numerous papers utilizing AMR.

Figure 1: Constant Mach surface and magnetic field lines for a coronal mass ejection (CME).

Adaptive Blocks

Figure 2: A two dimensional Adaptive Block Decomposition

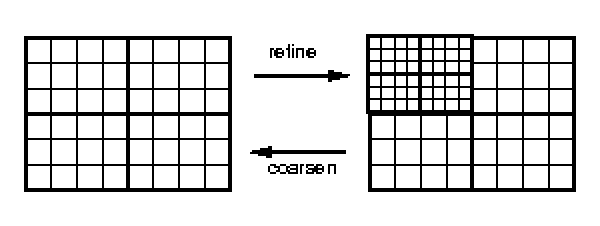
In general adaptive block approach, d-dimensional non-overlapping blocks are used to partition d-dimensional regions of interest. Each block is decomposed into a regular m₁ x m₂ x ... x m_d array of cells. When a block is refined, it is replaced by 2^d children, each again decomposed into a regular m₁ x m₂ x ... x m_d array. In each dimension, the extent of a child's cell is half that of the parent's cell. Coarsening is achieved by reversing this process and replacing the 2^d children by their parent. An adaptive block decomposition of a three-dimensional spatial domain is illustrated in Figure 3.

Figure 3: A three-dimensional adaptive block decomposition.

In contrast to adaptive blocks, Figure 4 illustrates a quadtree decomposition. In this cell-based tree decomposition, when a cell is subdivided, the child cells are created and the parent remains, so that the region of the original cell now has two representations. Generalized quadtrees and octrees have been widely used for a variety of two- and three-dimensional applications involving spatial decomposition ([5]). Note that the adaptive blocks for a decomposition of a two-dimensional domain are similar to the leaves of a quadtree decomposition, and in general the adaptive block decomposition of a d-dimensional domain are similar to the leaves of a d-dimensional generalized tree.

Figure 4: A quadtree decomposition.
Leaves are shown in green. Lines indicate parent-child links.

In the adaptive block data structure, inter-block connectivity is defined using pointers. Each block has pointers to the neighboring blocks with which it shares a face (in other implementations, one may also need pointers to blocks sharing lower dimensional ``faces'' such as edges and corners). Thus neighbor information is maintained explicitly. This is similar to the explicit maintenance of neighbor information in unstructured grids. In contrast, quadtree and octree data structures explicitly maintain only parent-child information and neighbor information must be obtained by a tree traversal.

Note that a block may have many neighbors along a given face, depending on the number of times refinement has occurred among the neighbors. In our applications, we restrict refinement so that neighboring blocks differ by at most one level of resolution. For example, in Figure 2 note the right hand side; if the upper right small block was refined it would cause the upper right large block to also be refined. Refinement can potentially cascade across the grid. For adaptive blocks with at most one level of resolution change between adjacent blocks, there are at most 2^d-1 blocks sharing a given face. If k levels of resolution change are permitted, then there can be as many as 2^{k (d-1)} blocks sharing a given face.

In our implementation of the adaptive block data structure, ``ghost'' cells are added around each block, to store values of cells in the neighboring blocks. For first-order accurate spatial operators only one layer of ghost cells is needed; for so-called ``higher-resolution methods'' ([6]), more layers of ghost cells are needed. Prolongation operations are used to determine ghost-cell values when the neighbor block is coarser than the block of interest; restriction operations are used when the neighbor is finer.

Adaptive Blocks versus Trees and Unstructured Grids

• Loop and cache optimizations can be performed over the arrays of cells in an adaptive block data structure. This is difficult, if not possible, with cell-based tree structures or unstructured grids. The use of ghost cells further enhances this advantage for calculations which depend on neighboring cell values.
• Adaptive blocks amortize the costs of neighbor pointers (both time and space) over entire arrays, and their ghost cell to computational cell ratio is far superior to other data structures.
• On parallel computers, adaptive blocks amortize the overhead of communication over entire blocks of cells, instead of over single cells as in tree data structures and unstructured grids.
• Adaptive blocks locate neighbors directly, as do unstructured grids, rather than using parent/child tree traversals to locate them as required in standard tree structures.
• Because adaptive blocks permit the refinement of larger multi-cell regions at one time, mesh adaptation need not occur as frequently as for data structures based on single cells. This reduces computational overhead.

However, adaptive blocks can also have some disadvantages when compared to the alternatives. When the size of the array of cells per block is very large, then

• Load balance on parallel computers is harder to maintain when refinement and coarsening occur dynamically and when there are far fewer blocks than cells such that there a small number of blocks assigned to each processor element. If the average number of blocks per processor is small and there are a large number of cells per block, then any processor having a number of blocks above the average will be doing significantly more work, causing the other processors to be delayed.
• Excessive numbers of refined cells can be created (i.e., typically more than the corresponding number of cells used in cell-based tree data structures) thereby increasing the amount of time and storage space needed.

The values of the m₁, ..., m_d parameters can be chosen to best trade off the advantages versus the disadvantages. For example, in our three-dimensional MHD implementation on the T3D, the values m₁ = m₂ = m₃ =16 were chosen as a reasonable compromise.

Figure 5: Time per cell as a function of block size.

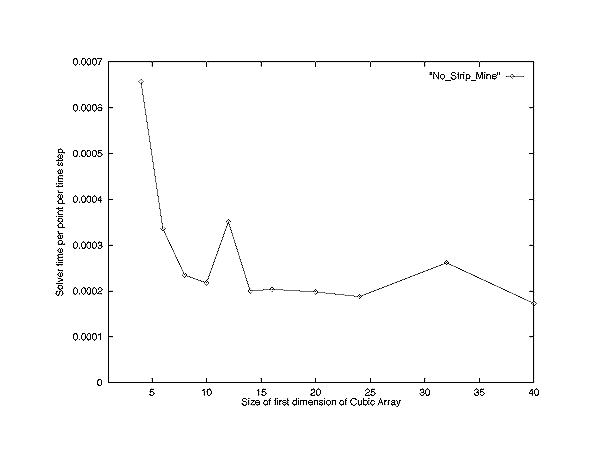
Figure 5 shows a plot of time per cell as a function of the number of cells per block for this implementation. (The smallest block is 2x2x2, rather than a single cell, because it would have required significant rewriting of code to time a true octree.) As can be seen, there is dramatic improvement initially as the size of the blocks increases, but then little additional improvement occurs. The initial improvement is the effect of loop optimizations, and the fact that consecutive cells are brought into cache together. As we had expected, this effect is very significant, more than a factor of 3 improvement over the 2x2x2 case (and far greater over the single cell case). Such improvement was the motivating factor in developing adaptive blocks. These types of loop optimizations are of use on a variety of high performance architectures.

The local maxima shown in the figure are believed to be caused by cache effects on the T3D. For example, the peak at 12³ can be removed by padding the array with an additional surface of cells. The peak at 32³ can be reduced by data mining the larger blocks into smaller ones; this yields better cache performance and is optimal at sub-block size 16³.

Parallel Performance

However, an aspect of adaptive blocks that is less favorable for parallel computation is the fact that there are far fewer blocks than cells. As noted above, for a given simulation this may result in a small average number of blocks per processor. In such a situation, any processor exceeding the average by only a small number of blocks will have a significant load imbalance, which will reduce parallel efficiency. Choosing overly large blocks will exacerbate this problem. Whenever refinement or coarsening occurs, load re-balancing should be performed to insure high performance.

One critical test of a data structure intended for parallel computers is the achieved scaling as the number of processors increases. In Figure 6 we show the scaleup achieved on the solar wind simulation ([2]) as the problem size was scaled linearly with the number of processors on a Cray T3D.

Figure 6: Parallel efficiency, scaling problem size with processors.

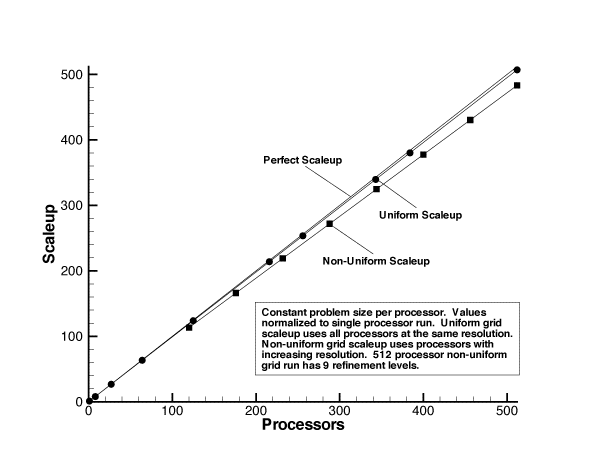
The efficiency is extremely high, even up to 512 processors. Further, the parallel efficiency is being compared to a single processor running adaptive blocks, which is significantly faster than a single processor solving the same problem using a cell based tree.

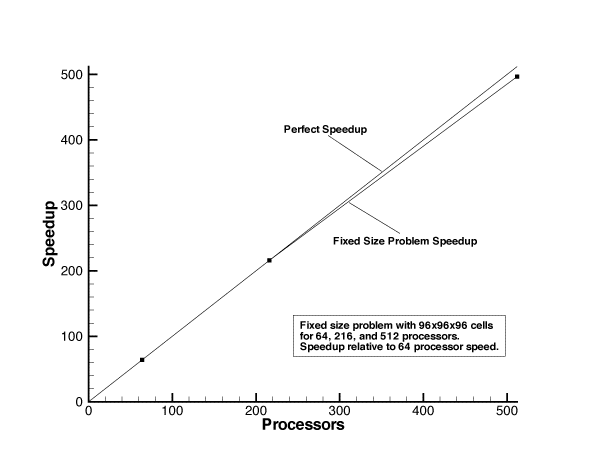
Another test of the parallel efficiency is the speedup for a fixed size problem. In Figure 7 we show this speedup. Note that it would have been impossible to test this problem on a single processor, because no single processor would have sufficient memory. The speedup here is relative to the 64 processor speed.

Figure 7: Parallel efficiency, fixed problem size.

Generalizations

• various orders of spatial accuracy can be achieved by varying the number of ghost cells around each block;
• the neighbor pointers can be extended to include blocks sharing low dimensional boundaries;
• the constraint on the relative refinements of neighbors can be loosened, allowing refinement level differences greater than one;
• the initial block configuration need not be Cartesian.

Finally, while our use of adaptive blocks has been motivated by their use in adaptive mesh refinement, the approach can be used for a variety of other problems involving spatial decomposition. Most of their performance advantages would carry over to a wide range of applications, especially when the block size is properly tuned.

Acknowledgment

References

2. T. I. Gombosi, K. G. Powell, Q. F. Stout, E. S. Davidson, D. L. De Zeeuw, L. A. Fisk, C. P. T. Groth, T. J. Linde, H. G. Marshall, P. L. Roe, B. van Leer, Multiscale modeling of heliospheric plasmas, High Performance Computing 1997.

3. R. M. Haberli, T. I. Gombosi, D. L. De Zeeuw, M. Combi, K. G. Powell, Modeling of cometary x-rays caused by solar wind minor ions, Science 8, May 1997.

4. J. Quirk, An Adaptive Grid Algorithm for Computational Shock Hydrodynamics, Ph.D. thesis, Canfield Institute of Technology, 1991.

5. H. Samet, The quadtree and related hierarchical data structures, Computing Surveys 16 (2), 1984.

6. B. van Leer, Towards the ultimate conservative difference scheme. V. A second order sequel to Godunov's method, Journal of Computational Physics 32, 1979.

Author Biographies

Quentin F. Stout is Professor of Computer Science. His research interests are in parallel computing, especially in the areas of scalable parallel algorithms and in overcoming inefficiencies caused by interactions among communication, synchronization, and load imbalance. This work has been applied to a variety of industrial and scientific parallel computing problems, as well as to fundamental problems in areas such as sorting, graph theory, and geometry. He is Co-Principal Investigator of the NASA HPCC ESS Computational Grand Challenge Investigator Team at the University of Michigan. Home Page.

Darren L. De Zeeuw is Assistant Research Scientist at the Space Physics Research Laboratory. His interests involve the development and implementation of algorithms to solve the multidimensional Euler and MHD equations using octree-based unstructured Cartesian grids with adaptive refinement and multigrid convergence acceleration. He is one of the primary developers of the code described in this paper. Home Page.

Tamas I. Gombosi is Professor of Space Science and Professor of Aerospace Engineering. He has extensive experience in solar system astrophysics. His research areas include generalized transport theory, modeling of planetary environments, heliospheric physics, and more recently, multiscale MHD modeling of solar system plasmas. He is Interdisciplinary Scientist of the Cassini/Huygens mission to Saturn and its moon, Titan. Professor Gombosi is Senior Editor of the Journal of Geophysical Research Space Physics. He is Program Director and Co-Principal Investigator of the NASA HPCC ESS Computational Grand Challlenge Investigator Team at the University of Michigan. Home Page.

Clinton P.T. Groth is Assistant Research Scientist at the Space Physics Research Laboratory. His research interests involve generalized transport theory and the development of higher-order moment closures for the solution of the Boltzmann equation via advanced numerical methods with applications to both rarefied gaseous and anisotropic plasma flows. This research has led to a new hierarchy of moment closures with many desirable mathematical features that appears to offer improved modeling of transitional rarefied flows. Home Page.

Hal G. Marshall is Associate Research Scientist at the Center for Parallel Computing and the Lab for Scientific Computation. He has interests in scientific computing using massively parallel computers. He is one of the primary developers of the code described in this paper. Home Page.

Kenneth G. Powell is Associate Professor of Aerospace Engineering. His research areas include: solution-adaptive schemes, genuinely multidimensional schemes for compressible flows, and, most recently, numerical methods for magnetohydrodynamics. He was a National Science Foundation Presidential Young Investigator from 1988-1994. He is Co-Principal Investigator of the NASA HPCC ESS Computational Grand Challlenge Investigator Team at the University of Michigan. Home Page.