Many years ago, I was teaching second-semester calculus in the Fall term. This class tends to have a bimodal distribution of students, some stronger in STEM fields, and some stronger in the humanities and social sciences. These students taught me an important lesson.
At one point, I was teaching a topic called "related rates", and I put the following problem on the board.
Two jets fly overhead at the same time.
One jet flies north at 400 mph.
One jet flies east at 300 mph.
One hour later:
How far apart are they?
How fast are they separating?
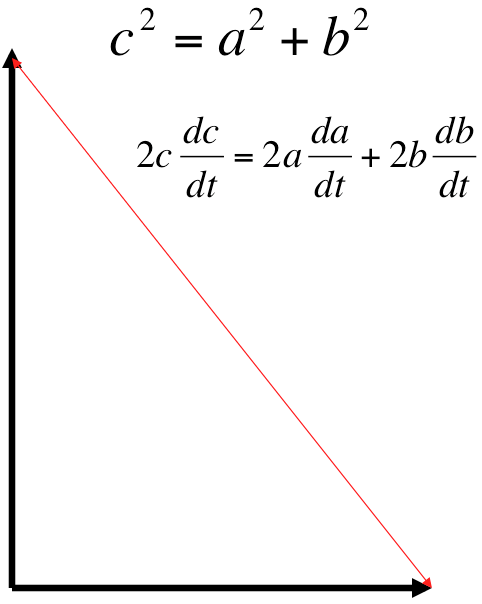
One group of students saw a right triangle, 400 miles on one side and 300 miles on the other. They also saw the Pythagorean Theorem, that lets them calculate that the hypotenuse is 500 miles (the first answer). And they knew (or learned) that the trick behind related rates problem is to differentiate the Pythagorean equation to get another equation involving rates (velocities), that they can solve for the second answer.

This is the answer I was looking for, that the Calculus class is trying to teach.
The second group of students had a very different response to this problem. They didn't see the right triangle and the Pythagorean Theorem.
They saw airplanes in the sky. And this led to a whole new set of questions.
Who's on board the plane?
Where did they come from?
Where are they going?
Why are they going there?
Do they have enough fuel to get there?
What will they do when they get there?
Where will they go after that?
Will they be able to get home?
A number of years ago (1959), British scientist and novelist C. P. Snow gave an important lecture that was published as a short book called The Two Cultures and the Scientific Revolution. (Very much worth reading!)
At the time, the problem was that the British intelligentsia only considered the humanities worthy of attention, and scorned the value of scientific knowledge. More than six decades later, the pendulum may have swung toward the other extreme.
Given a description of a situation . . .
One approach is to simplify the description to a skeleton that supports tractable inference.
Another approach is to make the description more complex by finding connections with other related situations.
Both of these approaches can provide powerful, useful conclusions. They complement each other, and can be used together. Often, useful abstractions can only be found after the original description of the situation has been expanded to include new factors. (Read "The Blind Men and the Elephant".)
Being able to use both approaches is important for everyone, but is especially important for research in artificial intelligence.