Metric-Space Indexes as a Basis for Scalable Biological Databases[1]
Daniel P. Miranker
1/19/03
Department of Computer Sciences
Center for Computational Biology and Bioinformatics
University of Texas
Austin, TX 78712
{miranker@cs.utexas.edu}
Abstract
Biological databases will be best served by the development of new specialized database management systems whose storage managers are based on metric-space indexing techniques and the development a database query languages that embody semantics derived from biological models of similarity and evolution.
Important biological data types cannot be effectively mapped to low dimensional coordinate systems on which O(log n) indexing methods rely. It is clear from an abundance of Bioinformatic discoveries that biological data is not random and exhibits interesting structure with respect to clustering. Metric–space indexing exploits a data set’s intrinsic clustering to speed the execution of similarity queries, even when the data cannot be mapped to a coordinate system. Database management systems that seamlessly integrate semantically rich query languages with a metric-storage and retrieval mechanism will allow biologists to simply and concisely develop informatic studies that have traditionally been large and labor intensive.
An Illusion in Current Practice
It is easy to mistake a large biological-data web site as a database management system (DBMS) or to anticipate that the software underlying a biological web site is a DBMS. A DBMS is a body of software that provides an integrated set of services on a collection of data, a database. Many popular biology web sites provide a number of services and their web-masters are usually careful to provide a common look-and-feel to each web page. Thus, an end user witnesses an integrated system. The reality is that each service is provided by an ad-hoc collection of scripted utilities and the underlying administration of the system rarely embodies generalized data management facilities.
These systems cannot be expected to scale, neither in performance as the volume of data increase, nor in ongoing software development costs as functionality is increased. Fast access to data in a relational database management system (RDBMS) requires ordinal data; e.g. numbers, dates, names etc. Biological data of primary importance does not fit the relational paradigm. This includes biological sequences, mass spectra, protein and ligand structures, phylogenetic and pathway graphs, to name a few.
When RDBMSs are used to manage biological data, first class data is relegated to blob and unstructured text fields. Annotations of the data, such as organism name and protein family name, may exist as part of the record. Relational tests against the annotations may be used to filter the database. Ultimately, mining of the biological data types is accomplished by utilities outside the database. Even when object-relational or semi-structured representations are used (e.g. ASN.1 and XML) there are few results in building persistent access paths capable of supporting sophisticated retrieval methods.
Consider two high profile examples, GenBank and TreeBASE [Genurl, Pie02]. Every web page in Genbank shares a common masthead. Argument structure and terminology is held consistent throughout the site. Thus, users witness an integrated set of services. Nevertheless sequence retrieval is accomplished using a utility, BLAST, which sequentially scans the entire sequence content of Genbank. Although Genbank is extensible through the use of ASN.1 descriptors, these descriptors face a manual curation process. When new tags are accepted by the curators, additional functionality does not automatically appear on the Genbank website.
TreeBASE serves as an archival repository of phylogenies. As in Genbank, a primary service of TreeBASE is to connect esoteric data to individual scientific articles that detail the investigation that derived the information. TreeBASE is built using an underlying relational database platform and embodies flexible and scalable query facilities for many needs. However, the phylogenies themselves are stored as a structured text strings known as Newick format [Felurl]. One drawback of using the Newick format is that the database cannot directly support queries concerning the relationships between the taxa and the structure of the phylogeny. In TreeBASE, queries specific to the structure of the individual phylogenies are done outside the database [Sha02]. An initial query may derive a subset of the phylogenies, but then each of those phylogenies is exported and handled outside the database. The utility has been integrated into the web site. The uninformed are unaware that the utility was not authored by the TreeBASE group or that it is running on a different server.
Storage and Similarity Search in Metric-Spaces
The concept of a metric-space moves the
attention away from the data to a distance function. Data structures that exploit metric space properties rely
only on the relative distance of objects to each other.
Definition: A metric space
is a set of objects, S, a [metric] distance function, d,
such that, given any three objects, x,
y, z in S, [Cha01]
(i) d(x,
y) >= 0 and d(x, y) = 0 iff x = y. (Positivity)
(ii) d(x, y) = d(y, x). (Symmetry)
(iii) d(x, y) + d(y, z) >= d(x, z). (Triangle Inequality)
All tree-based database index structures may be generalized as follows: Consider a dataset S of n objects. Arbitrarily partition S into blocks, such that the contents of each block can be qualified by a predicate P. For example, if the data type is rectangles on a plane, then P may be the minimum-bounding rectangle that covers all rectangles in the block. If there are B objects per block, roughly n/B blocks are created. Consider as a new data set the n/B predicates describing these blocks, and repeat the process until a single block, the root, is formed. The result is a balanced tree of height logB n.
For metric-space indexes, there are two primary methods used to define predicates: vantage points and generalized hyperplanes. In vantage point methods, bounding spheres are formed by identifying a center of the cluster (the vantage point) and a radius (the distance from the center to the furthest point in the cluster). In generalized hyperplanes, the equivalent of two center points are chosen. Membership of the remaining points to the partitions is determined by computing the distance of each point to the centers, and assigning the point to the closest center. The fan out may be increased by choosing many center points, in which case, in Euclidean space the data structure resembles a Voronoi partitioning [Bri95].
The value of a metric-space approach is that it is unnecessary to find a meaning for the data with respect to the axis of a coordinate system. There is a clear connection between algorithms for hierarchical clustering and the construction of a tree-based index structures. One can say that a tree-based index structure of a metric space materializes a persistent representation of a hierarchical clustering of the data [Cha01, Mao03].
Partitioning methods to form metric index trees exploit the triangle inequality to quickly identify naturally occurring data clusters and allocate them to separate sub-trees. A data point and a radius specify a similarity query. At each interior vertex of the index tree the query predicate is compared to the bounding predicate covering the data present in each subtree. The triangle-inequality is used to determine both if the query predicate overlaps the data in a subtree and to prune the number of distance calculations when visiting an interior node.
Similarity vs. Distance
A primary challenge in this thesis is the endemic use of similarity functions rather than distances. By this we mean, in most biological models of similarity, objects that are more similar are rewarded higher scores, an intuitively appealing result that reverses metric order. In the case of sequence alignment PAM and BLOSUM log-odds matrices contain negative values that can yield negative alignment scores. This violates positivity.
By using a main-memory metric index, Giladi et.al. have already reported two and three order of magnitude improvements in execution speed of sequence look-up compared to BLAST[Gil02]. However, their metric is simple Hamming distance, which is devoid of any model of evolution. By their own accounting, although fast, their result is limited in applicability to sequence assembly and studies between evolutionarily very close organisms.
“[N]othing in biology makes sense except in the light of evolution” Dobzhansky (1963)
Thus, to exploit metric-space search biological models of similarity must be revisited and new models that are metrics invented. In some cases, such as sequence alignment this is challenging. There is no simple algebraic normalization that will convert PAM matrices to a metric. However, the same assumptions and raw data as originally used to develop the PAM models can be revisited and a metric evolutionary model of evolution defined [Mao02]. In other cases simple algebraic normalizations may be sufficient.
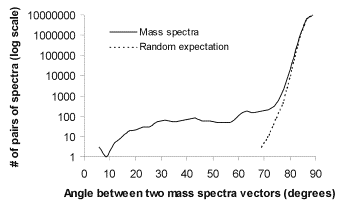
In Proteomics a common similarity measure used for database look-up of mass-spectra is shared peaks count. If we map mass-spectra to a vector-space model, one dimension for each resolvable peak, then the number of peaks shared by two spectra forms a similarity function computed by taking the inner-product of two spectra. In text retrieval systems it is understood that the corresponding metric is cosine distance. To test if spectra would cluster in a manner that would benefit from metric space indexing we assembled a database of computed mass-spectrometer spectra for the yeast proteome following trypsin digestion [Ppurl]. We then computed the cosine distance between all pairs of spectra. The results, plotted in Figure 1, indicate that the spectra are clearly not uniformly distributed in the space of spectra and show several local maxima much closer to zero degrees than expected by chance, which is evidence of clustering [Bri95].
Figure 1. Mass spectra of peptides
from the known yeast proteins show considerably more clustering than expected
by chance, indicating that spectra can be effectively organized in a
metric-space model.
Discussion
In an obvious ploy to draw analogy to the semiconductor industry it is often incorrectly stated that the growth of sequence data is exponential. The growth of biological data is hyper-exponential. The exponential improvements in semiconductors is a by-product of an established, regular cycle of process improvements. The genomic revolution is still in its infancy and the introduction of process improvements to automated laboratory apparatus is accelerating.
We recently passed a critical milestone. Where the doubling of the contents of Genbank has been reported as having a Moore’s constant of 18 months, equal to the doubling time of processor speeds, the doubling time for Genbank has shrunk to 15 months. Where computer-processing capacity was increasing faster than the computing demands of Bioinformatics, then equal to them, we can now anticipate a widening gulf between computational capacity and the demand of Bioinformatics.
Storage
and retrieval are the primary services required of a database management
system. It is arguable that the advent of the B+-tree and it effectiveness for
ordinal (1-dimensional) business data was critical to the initial success of
relational database management systems (R-DBMS). Subsequently, variations
of R-trees and k-d trees [Gae98] were developed to store and retrieve 2- and
3-dimensional data types and were instrumental in the creation of Geographic
Information Systems (GIS). Other fields have also found critical support
by virtue of specialized database management systems founded on different data
models and their supporting data structures. Examples include Computer Aided
Design (CAD), using object-oriented databases, and network management, using
the hierarchical database component of LDAP.
These precedents suggest to cope with the avalanche of unconventional biological data specialized database management systems must be invented. Metric-space indexing methods with concomitant development of metric models of biological similarity offer a promising approach.
References
[Bri95] S. Brin. Near neighbor search in large metric spaces. In Proc. VLDB'95, pages 574-584, 1995.
[Cha01] E. Chavez, G.
Navarro, R. Baeza-Yates, and J.L. Marroquin, Searching in Metric Spaces
(Survey).ACM Computing Surveys, 2001.
[Gae97] V. Gaede and O. Gunther. Multidimensional Access Methods. ACM Computing Surveys, 1997.
[Genurl] National center for biotechnology information. http://www.ncbi.nlm.nih.gov/
[Gil02] E. Giladi, M.G. Walker, J.Z. Wang, W.Volkmuth: SST: an algorithm for finding near-exact sequence matches in time proportional to the logarithm of the database size. Bioinformatics 18(6): 873-877 (2002)
[Mao02] R. Mao, D. P. Miranker, J. N. Sarvela and W. Xu. Clustering Sequences in a Metric Space. Poster on ISMB 02, Edmonton, Canada, August 2002.
[Mao03] R. Mao, W. Xu, N. Singh, D. P. Miranker. An Assessment of a Metric Space Database Index to Support Sequence Homology. Proceedings of the Third IEEE Conference on Bioinformatics and Bioengineering, 2003 (to appear).
[Pie02] W.H. Piel, M.J. Donoghue, and M.J. Sanderson. TreeBASE: a database of phylogenetic knowledge. In J. Shimura, K.L. Wilson, and D. Gordon, editors, To the interoperable ''Catalog of Life'' with partners, Species 2000 Asia Oceania, pages 41--47. 2002. Research Report from the National Institute for Environmental Studies No. 171, Tsukuba, Japan.
[Felurl] J. Felsenstein. The newick tree format. http://evolution.genetics.washington.edu/phylip/newicktree.html.
[Ppurl] Protein Prospector http://prospector.ucsf.edu/
[Sha02] H. Shan, K.G. Herbert, W.H. Piel, D. Shasha, and J.T.L. Wang. A structurebased search engine for phylogenetic databases. In 14th International Conference on Scientific and Statistical Database Management, pages 7-10, 2002.