Research Projects
Please note that this list of projects has not been update
for a number of years. It is, however, indicative of the type
research that I am undertaking.
Inverse Problems in Power System Dynamics
Analysis of Uncertainties in Power System
Simulation
Power System Parameter Estimation
Stability of Limit Cycles in Hybrid Systems
Stability and Optimization of Transformer Tapping
Optimal Load Shedding to Alleviate Voltage Instability
Parameter Values that Induce Marginal Stability
Last updated 25 April 2001
Inverse
Problems in Power System Dynamics
Analysis of power system dynamic behavior frequently takes the form of inverse problems, where the aim is to find parameter values that achieve (as closely as possible) a desired response. Examples include parameter estimation, quantifying parameter uncertainty, boundary value problems, and optimal control. The project is developing algorithms for solving such inverse problems. Power system behavior inherently involves interactions between continuous dynamics and discrete events. A systematic hybrid systems framework for modeling, analysis and algorithms is being pursued.
Trajectory Sensitivity Analysis of Hybrid Systems
The development of trajectory sensitivity analysis for hybrid systems, such as power systems, is the main focus of this research. Crucial to this analysis is the development of jump conditions describing the behavior of sensitivities at discrete events such as switching and impulse action. Trajectory sensitivities can be computed efficiently as a by-product of numerical simulation, and underlie gradient-based algorithms for solving inverse problems. The project is extending earlier analysis to systems that contain variable time delays.
Following a large disturbance, trajectory sensitivities tend to exhibit more pronounced transient behavior than the underlying trajectory. The project is investigating ways of exploiting this phenomenon as an indicator of impending instability. Of particular interest is the role played by the principal singular surface (PSS). As a trajectory evolves, the transient Jacobian of the flow becomes singular on the PSS. Within the principal region (bounded by the PSS), trajectory sensitivities contract. Beyond the PSS, sensitivities expand, but typically in a single dimension related to the separation mode.
Analysis of Uncertainties in Power System Simulation
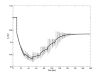Parameters of power system models can never be known
exactly, yet dynamic security assessment relies upon simulations derived from
those uncertain models. This project is exploring ways of quantifying the
uncertainty in simulations of power system dynamic behavior. Trajectory
sensitivities can be used to generate an accurate first order approximation of
the trajectory corresponding to a perturbed parameter set. Therefore it is
feasible to quickly generate many approximate trajectories from a single nominal
case. Monte-Carlo techniques can be used to estimate the statistics describing
the effects of parameter uncertainty.
Power System
Parameter Estimation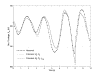
The nonlinear non-smooth nature of power system dynamics complicates the process of validating system models from disturbance measurements. This project is investigating algorithms for computing a set of model parameters that provide the best fit between measurements and model response. Trajectory sensitivities are used to identify parameters that can be reliably estimated from available measurements.
Stability of Limit Cycles in Hybrid Systems
Limit cycles are common in hybrid systems. However the non-smooth dynamics of such systems makes stability analysis difficult. We have been using recent extensions of trajectory sensitivity analysis to obtain the characteristic multipliers of non-smooth limit cycles. The stability of a limit cycle is determined by its characteristic multipliers. Numerous applications have been explored, ranging from on/off control of coupled tanks, through power electronic circuits, to the walking motion of a biped robot. Period-doubling bifurcations have been explored in these latter cases.
Multi-layer Systems
Communications networks play a significant role in the multi-layer representation of power systems. The communications network model being proposed is based on a conceptual abstraction involving finite channel and node capacities that trigger changes in message transmission delays. Numerical integration of systems that incorporate such variable time delay models is not straightforward. This is especially so when considering the switched (hybrid) nature of system behavior. The project is investigating various techniques to handle variable time delays within numerical integration techniques. An important criterion is that algorithms must be capable of efficiently computing trajectory sensitivities.
Stability and Optimization of Transformer Tapping
Discrete
events introduced by on-load tapping of transformers can have a significant
affect on the load-end dynamic behavior of power systems. This project is taking a hybrid
systems approach to quantifying that behavior. Of particular interest is the
stability of systems that involve cascaded tapping transformers. Limit cycles
have been observed in such systems. Stability theory for switched ODE systems is
being adapted to switched DAE systems, which are more common in power system
applications. The project aims to devise optimal switching control strategies
for minimizing tap-changer hunting.
Optimal Load Shedding to Alleviate Voltage Instability
Load shedding provides an effective (though drastic) control strategy for alleviating voltage instability. However the disruption to consumers caused by load shedding should be minimized. This project is developing optimal control techniques that are applicable in this hybrid system setting. The aim is to determine locations and shedding times that minimize the total shed load.
Parameter Values that Induce Marginal Stability
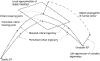Stability
limits place restrictions on power system operations. Calculation of these
limits is therefore very important, but is also quite difficult. This project is
exploring algorithms for determining parameter values that result in marginal
stability of a system. (A system is marginally stable for a particular
disturbance if the post-disturbance trajectory lies on the stability boundary.)
A nonlinear least-squares formulation has been developed to determine a critical
set of parameter values. Other approaches that are based on boundary-value
problems are being explored.
In order to maintain marginal stability, perturbations in some parameters must be matched by compensating changes in other parameters. The project is developing sensitivity relationships between the two groups of parameters. These sensitivities form the predictor in a predictor-corrector continuation method for tracing the parameter space view of the stability boundary.
Power Flow Solution Space
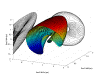Knowledge of the structure of the
power flow solution space is important when analyzing the robustness of
operating points. Unfortunately, that structure has not been clearly
established. As part of this project, a predictor-corrector technique has been
developed to assist in exploring the solution space boundary. Using that
technique, it has been found that the solution space may contain holes, even for
very simple systems. This project is characterizing the solution space structure
for various sub-classes of systems. The ultimate aim is to see how far those
results can be extended for general systems.