EECS 658_________________________PROBLEM SET #2_________________________Fall 1999
ASSIGNED: Sept. 23, 1999. READ: Convolutions handout given out on Thursday Sept. 23.
DUE DATE: Sept. 30, 1999. THIS WEEK: Chinese remainder theorem, Euclidian algorithm.
    1. A very simple application of the polynomial Chinese remainder theorem:
    1. Show that the solution to M(z)X(z)=1 mod(z-a) is X(z)=1/M(a), provided M(a) isn't 0.
      This is useful for the polynomial Chinese remainder theorem solution procedure.
    2. Show you can formulate the interpolation problem X(zi)=ci as: X(z)=ci mod(z-zi), i=1...n.
    3. Apply the Chinese remainder theorem to derive the Lagrange interpolation formula.
  2. Apply Winograd to derive a fast algorithm for multiplying quadratic polynomials mod(z³ -8):
    y0+y1z+y2z²= (h0+h1z+h2z²) (u0+u1z+u2z²) mod(z³ -8).
    HINTS: (1) z3-8=(z-2)(z² +2z+4); (2) z² +2z+4=(z-2)(z+4)+12.
    You can use the latter hint to avoid the Euclidian algorithm for polynomials, if desired.
    3. We wish to multiply (3458)(2992) using residue number systems (illustrative example).
      Use as moduli: 2,3,5,7,11,13,17,19; their product is about 10 million (large enough).
    1. Compute the residues of 3458 and 2992 for each modulus (total of 16 numbers).
    2. Compute the residues of the product for each modulus (total of 8 numbers).
    3. Use the Chinese remainder theorem to compute (3458)(2992). Confirm this is right.
  4. Blind deconvolution of integer sequences (useful for sequences scaled to integers):
    We observe yn=hn*un={143,96,199,97,217,199,274,156,146,114,78,83,34,11,1}.
    GOAL: To reconstruct BOTH hn and un from their convolution yn (2 unknowns).
    All we know is hn and un are scaled to positive integers, 0 < h,u < 10, n > 0.
    Compute hn and un. HINT: Use the Euclidian algorithm repeatedly, and 143=(13)(11).
  5. Multichannel blind deconvolution (this is presently a "hot" topic; see journals):
    We observe yn¹=hn*un¹={1,13,78,286,715,1287,1716,1716,1287,715,286,78,13,1}
    and observe yn²=hn*un²={1,7,23,49,80,112,144,176,199,185,121,47,8}.
    GOAL: Compute hn,un¹,un² from yn¹,yn².
    These sequences need NOT be integer-valued; we know NOTHING except that WLOG h0=1.
      Compute hn, un¹ and un² in three ways (which one is easiest?):
    1. By finding the common zeros of Y¹(z) and Y²(z), and using them to compute H(z).
      Don't be surprised if this doesn't work well; how do you identify exactly common zeros?
    2. By applying the Euclidian algorithm for polynomials to Y¹(z) and Y²(z).
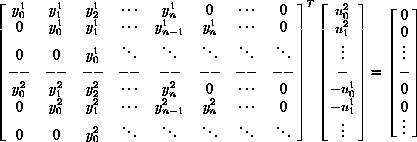
    3. By writing Y¹(z)U²(z)-Y²(z)U¹(z)=0 as the linear system of equations