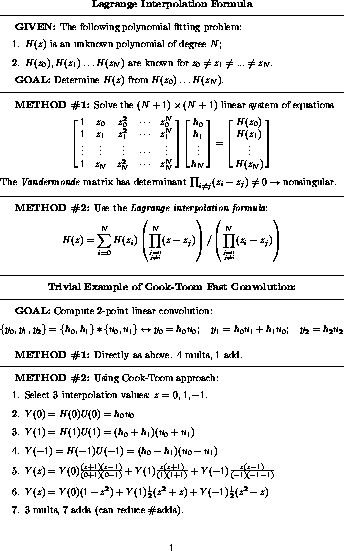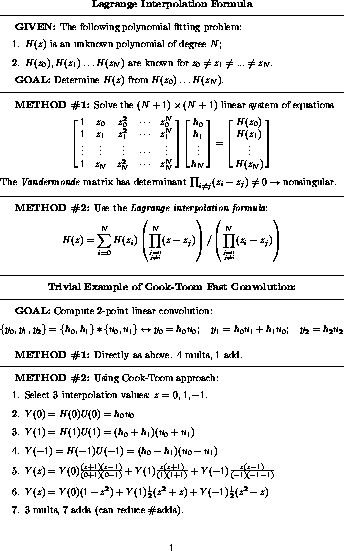EECS 658 THE FIRST LECTURE Fall 1999
Introduction to the course:
- Went over Introductory Handout.
- Went over Course Announcement.
- ASSUME: You know DFTs and convolutions are useful.
What can we do with Fast Algorithms?
- Combine smaller algorithms into larger algorithms
OR: Split up large problem into smaller ones: Divide
- Use very efficient small algorithms: Conquer
- Develop new ways of solving problems: Applications
Examples: (Numbers correspond to those above)
Combine smaller into larger:
- Cooley-Tukey FFT: 2D DFT to 1D DFT (twiddle mults)
- Good-Thomas FFT: 2D DFT to 1D DFT (no twiddle mults)
- Winograd Convs: Chinese Remainder thm. for polynomials
- Block matrix multiplication: large to smaller.
- POINT: When nesting small algorithms into large ones,
reducing #mults is much more important than reducing #adds,
although mults and adds take same time. Will see why later.
Efficient small algorithms:
- Direct computation of small DFTs (ugh).
EXAMPLE: 5-point DFT using 16 complex mults.
- Prime Factor FFT: (p)point DFT to (p-1)point cyclic conv.
EXAMPLE: 5-point DFT to 4-point cyclic convolution.
POINT: 4 complex mults, instead of 16 complex mults.
- Cook-Toom fast small convolutions (trivial example below)
(also useful for Mallat's fast wavelet algorithm).
- Strassen's fast 2× 2 matrix multiplication.
Applications:
- 2D bandwidth extrapolation of finite-support image (see below).
- Phase retrieval and blind deconvolution.
- Inverse scattering (reconstruction from reflections).