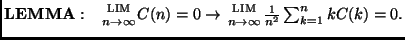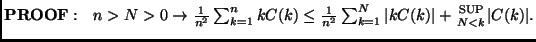- Use the result of Problem Set #5, Problem #6 in this problem (Rx(i,j)=autocorrelation):
- Two zero-mean random sequences x(n) and y(n) have the interesting property:
Rx(n,n)+Ry(n,n)=2Rxy(n,n). What can you say about sequences x(n) and y(n)? - A zero-mean WSS random sequence x(n) has Rx(T)=Rx(0) for some constant T.
Show (with probability one) that x(n) and Rx(n) are both periodic with period T.
Let e=1-p approach zero and use: (1-e)|m-n|=1-e|m-n| and (m+n)-|m-n|=2 MIN[m,n].
Compare this to the result from lecture: An II process is the sum of an iid process.
HINT: x(n)=px(n-1)+w(n),x(0)=0 becomes x(n)=h(0)w(n)+...+h(n-1)w(1), h(n)=pn.
Define two new random sequences N(n)=x(1)+x(2)+...+x(n) and Y(n)=(-1)N(n).
Compute the mean function and the covariance function of both N(n) and Y(n).
Are either of the random sequences N(n) or Y(n) WSS or asymptotically WSS?
x(n,s) is the basic definition of a random process: A mapping with domain (time)X(sample space).
In x(n,s) the random variable s has pdf fs(S)=1 if 0 < S < 1; fs(S)=0 otherwise.
- Note the pmf for x(n) is given by: Pr[x(n)=n]=1/n; Pr[x(n)=0]=1-1/n.
- Show that x(n) converges to 0 in probability (you don't need x(n,s) for this; only the pmf).
- Show that x(n) converges to 0 with probability one (you DO need x(n,s) for this).
- Show that x(n) does NOT converge to 0 in mean square (you don't need x(n,s) for this).
HINT: There is virtually NO computation in this problem! Just THINK (uh-oh!).
Let M(n)=[x(1)+x(2)+...+x(n)]/n=sample mean, and C(n)=[R(1,n)+R(2,n)+...+R(n,n)]/n.
PROVE that M(n) converges in mean square to E[x]=0 IFF C(n) goes to 0 for large n.
This ergodic theorem doesn't require x(n) to be iid, just asymptotically uncorrelated.
Compare this to the weak law of large numbers: M(n) converges in probability to E[x] if x(n) iid.
HINT: ONLY IF: Apply the Cauchy-Schwarz inequality to C(n)=E[M(n)x(n)].
HINT: IF: Show Var[M(n)]=[R(1,1)+...+R(1,n)+R(2,1)+...+R(n,n)]/n2 (see (6.1-10) on p. 273) and