EECS 501__________________________PROBLEM SET #3__________________________Fall 2001

---

ASSIGNED: Sept. 21, 2001. Read Stark and Woods pp. 60-119 on various pdfs.
DUE DATE: Sept. 28, 2001. THIS WEEK: pdfs and PDFs and sample spaces.

---

1. Stark and Woods #2.2. A simple PDF and pdf problem. Your sketches should be neat.

   ---

2. Prove for n=3 only (not for general n) the principle of inclusion and exclusion:
   
   1. 
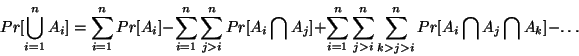
      Use this result and some permutations/combinations to solve the following problem:
   2. An absent-minded professor (no one you know) wrote n letters and sealed them in
      envelopes without writing the addresses on the envelopes. Having forgotten which letter he
      had put into each envelope, he wrote the n addresses on the n envelopes entirely at random.
      Compute Pr[at least one envelope was addressed correctly].
      HINT: Let A_i=Pr[i^th envelope addressed correctly]. What happens as n goes to infinity?

   ---

3. Random variables x,y,z,w have the joint pdf below. Compute the pdf f_x|w,y,z(X|W,Y,Z).
   

   ---

4. Let a,b,c > 0 be independent random variables, each with pdf f_x(X) and PDF F_x(X). Show:
   

   ---

5. Two real numbers b and c are chosen at random and independently of each other.
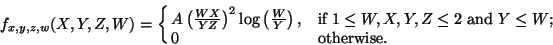
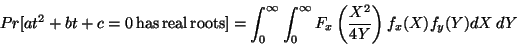
   Compute Pr[the quadratic equation t²+bt+c=0 has two real roots] as follows:
   Let b and c each be chosen from the interval [-n,n] and solve the problem for some finite n
   (draw your picture carefully--it's tricky!). What happens as n goes to infinity?

   ---

6. The rejection technique is a procedure for generating random numbers with a desired pdf f_x(X):
   Let f_x(X) be nonzero only for 0 < X < 1, and have maximum value f_m. Do the following:
   • Spin a wheel of fortune repeatedly; group the resulting numbers into pairs (X_i,Y_i)
   • Keep X_i only if f_x(X_i) > f_mY_i; otherwise discard it.
   The problem for you is to do the following:
   1. Show that the accepted X_i have pdf f_x(X). (This is a conditional marginal pdf problem.)
   2. Write a simple Matlab program that uses the rejection technique to generate
      random numbers distributed with the parabolic pdf f_x(X)=3X², 0 < X < 1.
      Use Matlab's hist to create a histogram (bar graph) of the number of accepted X_i.
      Turn in: Matlab code and histogram. Use 20 bins and 4000 random number pairs.

   ---

   "A chicken is an egg's way of making another egg"--anonymous.