EECS 501__________________________PROBLEM SET #2__________________________Fall 2001

---

ASSIGNED: Sept. 14, 2001. Read Stark and Woods pp. 13-36 and 52-60.
DUE DATE: Sept. 21, 2001. THIS WEEK: Conditional probability and combinatorics

---

1. Stark and Woods #1.24. A "story" problem (actually very simple).
2. Stark and Woods #1.25. A simple conditional probability problem.
3. Stark and Woods #1.35. Also show both answers reduce to mp when p < < 1 and N=1.
4. Stark and Woods #1.15. Do this in sample space--don't get fancy!
5. Stark and Woods #1.16. A simple Bayes's rule problem.

   ---

6. From the A.W. Drake book (see what I mean about not missing it?):
   • Die A has 5 olive faces and 1 lavender face;
   • Die B has 3 olive faces and 3 lavender faces.
   • However awful their face colors may be, both dice are known to be fair.
   • A fair coin is flipped once. Then:
     • If it falls heads, throw die A n+1 times;
     • If it falls tails, throw die B n+1 times.
   1. Compute Pr[nth throw of whichever die is used is olive].
   2. Compute Pr[nth AND (n+1)st throws of the die are both olive].
   3. Given that the first n throws of the die all resulted in olive, compute the conditional
      probability that the (n+1)st throw will result in olive. Interpret your result for large n.

   ---

7. A combinatorical interpretation of a mathematical identity:
   1. k balls are selected at random from a box containing n white balls and m black balls.
      Compute Pr[r of the k balls are white].
   2. Use the result of (a) to compute the sum:
      

   ---

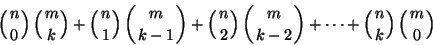
   Q: What do the Detroit Lions and evangelist Billy Graham have in common?
   A: Both can make 80,000 people scream "Jesus Christ!" simultaneously.