EECS 210_________________________PROBLEM SET #5________________________Winter 2001
ASSIGNED: February 09, 2001. Read: Chapter 5 of text and Chapter 1 of Additional Course Notes.
DUE DATE: February 16, 2001. In Lab Book: Read material on the Lab Exam, which is THIS WEEK.
    THIS WEEK: Thevenin and Norton equivalents and maximum power transfer.
  1. Text #4.55. EXTRA: See Additional Course Notes, pages 54-55, for more automobile loads.
  2. Text #4.58. 1 node equation in 1 unknown for each of VOC and ISC. Note (b) is a check on (a).
  3. Text #4.62. HINT: Simplify the leftmost 3 elements and do a Thevenin-to-Norton xform.
  4. Text #4.69. Apply a 1V voltage source and compute current (1 node equation in 1 unknown).
  5. Text #4.71a. The basic idea behind maximum power transfer--what it is and what it isn't.
    Now redo this problem with the 6 Ohm resistor and variable Ro exchanged (Ro is now the load).
  6. For #4.62, what load resistance connected to terminals a-b dissipates the most power?
    7. Why bother with Thevenin equivalents? Try this problem with a nonlinear device:
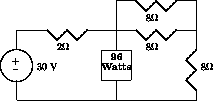
      We wish to compute the voltage and current for the 96-watt light, which is NOT a resistor!
    1. Compute the Thevenin equivalent of the circuit connected to ("seen by") the light.
    2. Use KVL to obtain a quadratic equation for the current through the light (or its voltage).
    3. Compute the voltage and current for the light. Note there are two correct answers!
      HINT: Regard the 96-watt light as having the nonlinear i-v characteristic i=96/V.
"The difference between a halo and a noose is about one foot"