EECS 210_________________________PROBLEM SET #2________________________Winter 2001

---

ASSIGNED: January 12, 2001. Read Chapter 1 of the textbook (this is not needed for problems below).
DUE DATE: January 19, 2001. In Lab Book: Lab Exp't #1; Unit #2 on measuring voltage and current.

---

THIS WEEK: Basics of the frequency response of systems and its effect on signals.
Attach a printout of the Matlab computer code you used to generate both of your plots.

---

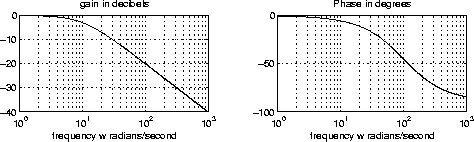
1. A linear time-invariant system has the gain and phase responses plotted below.
   Note that gain is in decibels, phase is in degrees, and frequency is in radians/second.
   
   1. Compute the output signal if the input signal is: (i) cos(100t); (ii) 7+3cos(100t+20°).
   2. Compute the input signal if the output signal is: (i) cos(100t); (ii) 7+3cos(100t+20°).

   ---

2. A periodic signal with period T=3 has Fourier series amplitudes c_n and phases ø_n in radians:

   n	0	1	2	3	4	5	6	7	8	9	10
   cn	6.3	5.4373	2.9302	1.9832	1.4954	1.1992	1.0005	0.8581	0.7511	0.6677	0.6010
   øn	0	-1.1425	-1.3709	-1.4646	-1.5208	-1.5616	-1.5946	-1.6231	-1.6488	-1.6726	-1.6951

   Plot the sum of the first 11 terms of the Fourier series. What function is this approximating?

   ---

3. A linear system has gain function of the form: GAIN(w)=B/(w²+A²); PHASE(w)=0.
   Here w is angular frequency in radians/second and A and B are unknown constants.
   The response of the system to 3cos(2t)+5cos(8t) is 15cos(2t)+10cos(8t). Compute A and B.

   ---

4. HINT: Use symmetry to cut your work in half, since this is an even function.
   1. Compute the Fourier series expansion of the triangle wave shown below.
      
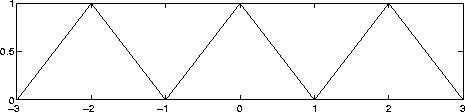
   2. This signal is passed through a "brick-wall" low-pass filter, which passes
      with no effect all frequencies below 2 Hz and rejects all frequencies above 2 Hz.
      Plot the output using Matlab. Explain why the corners have been rounded.

   ---

   "A chicken is an egg's way of making another egg"--Anonymous